Matemática 8º ano
-
8.1 Números reais5 Tópicos|5 Questionários
-
8.2 Cálculos algébricas5 Tópicos|5 Questionários
-
8.3 Equações e inequações4 Tópicos|4 Questionários
-
8.4 Produtos Notáveis1 Tópico|1 Questionário
-
8.5 Triângulos11 Tópicos|11 Questionários
-
Ponto reta e plano
-
Ângulos complementares Suplementares e Bissetriz
-
Ângulos opostos pelo vértice
-
Ângulos formados por duas retas e uma transversal
-
Classificação de triângulos
-
Ângulos externo do triângulo
-
Congruência de triângulos
-
Triângulo retângulo
-
Pontos notáveis do triângulo
-
Triângulos isósceles
-
Triângulos equiláteros
-
Ponto reta e plano
-
8.6 Quadriláteros9 Tópicos|9 Questionários
-
8.7 Circunferência6 Tópicos|6 Questionários
-
8.8 Estatística e probabilidade4 Tópicos|4 Questionários
Potenciação e notação científica
Potenciação:
Expressa o mesmo número sendo multiplicado diversas vezes. Veja o exemplo: 52 = 5 x 5 =25.
Nesse caso, tem-se uma base e o expoente, no nosso exemplo a base foi 5 e expoente foi 2. Podemos expressa-la da seguinte forma:
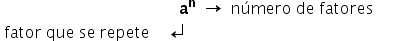
Vamos ver alguns exemplos: 3 x 3 = 32 = 9
Para essa situação, temos: dois (3) é a base, três (2) é o expoente e o resultado da operação, oito (9), é a potência.
Propriedades da potenciação
- Produto de potências de mesma base: repete-se a base e somam-se os expoentes.
Exemplo: 24 x 25 =2 4+ 5 = 2 9
2. Divisão de potências de mesma base: repete-se a base e subtraem-se os expoentes.
Exemplo: 24 ÷ 25 =2 4- 5 = 2 -1
3. Potência de potência: mantém-se a base e multiplicam-se os expoentes.
(24)5 =2 4x 5 = 220
- Distributiva em relação à multiplicação: multiplicam-se as bases e mantém-se o expoente.
Exemplo: 24 x 34 = (2 x 3) 4 = 64 = 1296
- Distributiva em relação à divisão: dividem-se as bases e mantém-se o expoente.
Exemplo: 24 ÷ 34 = (2 ÷ 3) 4 = 4/9
Exercícios resolvidos:
1 – Determine o valor de cada uma das potências abaixo.
a) 251
b) 1500
c) (7/9)-2
Resposta:
a) Quando uma potência está elevada ao expoente 1, o resultado é a própria base. Portanto, 251 = 25.
b) Quando uma potência está elevada ao expoente 0, o resultado é o número 1. Portanto, 1500 = 1.
c) Neste caso, temos uma fração elevada a um expoente negativo. Para resolvê-la devemos inverter a base e mudar o sinal do expoente.
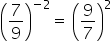
Agora, podemos elevar o numerador e o denominador ao expoente 2.
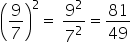
2 – As potências (-2)4 e -24 são iguais ou diferentes? E qual o resultado?
Resposta:
As potências são diferentes e apresentam como resultados 16 e -16, respectivamente.
Quando a base de uma potência é um número negativo e está elevada a um expoente par, o resultado será positivo. Entretanto, para sinalizar que a base é negativa seu valor deve estar entre parênteses.
(- 2)4 = (- 2) x (- 2) x (- 2) x (- 2) = +16
Quando não há parênteses separando a base, deve-se incluir o sinal de negativo no resultado.
– 24 = – 16
Portanto, os resultados são: (- 2)4 = 16 e – 24 = – 16.
– Notação científica: é uma forma de escrever números usando potência de 10. É utilizada para reduzir a escrita de números que apresentam muitos algarismos.
Um número em notação científica apresenta o seguinte formato:
N . 10n
Sendo,
N um número real igual ou maior que 1 e menor que 10;
n um número inteiro.
Exemplos
a) 6 590 000 000 000 000 = 6,59 . 10 15
b) 0, 000000000016 = 1,6 . 10 – 11
Transformar os números em notação científica de forma prática:
1º Passo: Escrever o número na forma decimal, com apenas um algarismo diferente de 0 na frente da vírgula.
2º Passo: Colocar no expoente da potência de 10 o número de casas decimais que tivemos que “andar” com a vírgula. Se ao andar com a vírgula o valor do número diminuiu, o expoente ficará positivo, se aumentou o expoente ficará negativo.
3º Passo: Escrever o produto do número pela potência de 10.
Exemplos
1) 32 000 = 3,2 . 104
2) A massa de um elétron é de aproximadamente 0,000000000000000000000000000911 g = 9,11 . 10 – 28 g

sim