Os conjuntos numéricos reúnem diversos conjuntos cujos elementos são números.
– Conjunto dos Números Naturais (N): ele reúne os números que usamos para contar (incluindo o zero) e é infinito.
Subconjuntos dos Números Naturais
N* = {1, 2, 3, 4, 5…, n, …} ou N* = N – {0}: conjuntos dos números naturais não-nulos, ou seja, sem o zero.
Np = {0, 2, 4, 6, 8…, 2n, …}, em que n ∈ N: conjunto dos números naturais pares.
Ni = {1, 3, 5, 7, 9…, 2n+1, …}, em que n ∈ N: conjunto dos números naturais ímpares.
P = {2, 3, 5, 7, 11, 13, …}: conjunto dos números naturais primos.
– Conjunto dos Números Inteiros (Z): reúne todos os elementos dos números naturais (N) e seus opostos. Assim, conclui-se que N é um subconjunto de Z (N ⊂ Z):
Subconjuntos dos Números Inteiros
Z* = {…, –4, –3, –2, –1, 1, 2, 3, 4, …} ou Z* = Z – {0}: conjuntos dos números inteiros não-nulos, ou seja, sem o zero.
Z+ = {0, 1, 2, 3, 4, 5, …}: conjunto dos números inteiros e não-negativos. Note que Z+ = N.
Z*+ = {1, 2, 3, 4, 5, …}: conjunto dos números inteiros positivos e sem o zero.
Z – = {…, –5, –4, –3, –2, –1, 0}: conjunto dos números inteiros não-positivos.
Z*– = {…, –5, –4, –3, –2, –1}: conjunto dos números inteiros negativos e sem o zero.
– Conjunto dos Números Racionais (Q): reúne todos os números que podem ser escritos na forma p/q, sendo p e q números inteiros e q≠0.
Q = {0, ±1, ±1/2, ±1/3, …, ±2, ±2/3, ±2/5, …, ±3, ±3/2, ±3/4, …}
Note que todo número inteiro é também número racional. Assim, Z é um subconjunto de Q.
Importante ressaltar que as dízimas periódicas são números racionais. Elas são números decimais que se repetem após a vírgula, por exemplo: 1,4444444444… Embora possua infinitas casas decimais, pode ser escrito como a fração 13/9.
Subconjuntos dos Números Racionais
Q* = subconjunto dos números racionais não-nulos, formado pelos números racionais sem o zero.
Q+ = subconjunto dos números racionais não-negativos, formado pelos números racionais positivos e o zero.
Q*+ = subconjunto dos números racionais positivos, formado pelos números racionais positivos, sem o zero.
Q– = subconjunto dos números racionais não-positivos, formado pelos números racionais negativos e o zero.
Q*– = subconjunto dos números racionais negativos, formado números racionais negativos, sem o zero.
Questões resolvidas:
1 – Analise os conjuntos a seguir e os relacione com os conjuntos descritos nas sentenças I, II e III.
A = {0,2,4,6,8,10…}
B = {1,3,5,7,9,11…}
C = {1,2,4,8}
I – Conjunto dos números ímpares
II – Conjunto dos divisores de 8
III – Conjunto dos números pares
Ao relacionar o conjunto com as sentenças, temos que:
A) A – I; B – II; C – III.
B) A – III; B – II; C – I.
C) A – I; B – III ; C – II.
D) A – III; B – I; C – II.
E) A – II; B – I; C – III.
Respostas:
A – III. Note que o conjunto A é composto por todos os números pares.
B – I. Já o conjunto B é composto por todos os números ímpares.
C – II. Os números que compõem o conjunto C são os divisores de 8.
2 – Efetue as expressões numéricas:
a) 2 +4 – 2 =
b) 2 {3 + 1 [5 – 4 (3. 2)] – 8}=
c) – 2 + 6 – 10 – 4 =
Resposta: a) 2 + 4 – 2 = (Resolva a expressão numérica da esquerda para direita)
2 +4 – 2 = 6 – 2 = 4
b) 2 {3 + 1 [5 – 4 (3. 2)] – 8} (Resolva a expressão numérica da esquerda para a direita e lembre-se de que primeiro são parênteses ( ), depois colchetes [ ] e, por último, chaves { }.
2 {3 + 1 [5 – 4 (3. 2)] – 8}= 2 {3 + 1 [5 – 4 (6)] – 8} = 2 {3 + 1 [5 – 24] – 8} = 2 {3 + 1 [-19] – 8} =2 {3 – 19 – 8} = 2 {3 – 27} = 2 {– 24} = – 48
c) – 2 + 6 – 10 – 4 = (Resolva a expressão numérica da esquerda para direita)
– 2 + 6 – 10 – 4 = 4 – 10 – 4 = – 6 – 4 = – 10
3 – Represente as frações na forma decimal.
a) 12/5
b) 47/8
c) 9/4
Respostas:
a)
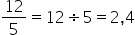
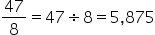
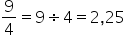

Respostas