Matemática 7º ano
-
7.1 Números inteiros3 Tópicos|4 Questionários
-
7.2 Números racionais3 Tópicos|3 Questionários
-
7.3 Potenciação e radiciação2 Tópicos|2 Questionários
-
7.4 Cálculos Algébricos2 Tópicos|2 Questionários
-
7.5 Equações e inequações3 Tópicos|3 Questionários
-
7.6 Ângulos e retas7 Tópicos|7 Questionários
-
7.7 Áreas e transformações4 Tópicos|4 Questionários
-
7.8 Regra de Três5 Tópicos|5 Questionários
-
7.9 Estatística e Probabilidade4 Tópicos|4 Questionários
Conjunto dos números inteiros 7º ano Curso
Números Inteiros
Os números inteiros são os números positivos e negativos, que não apresentam parte decimal e, o zero. Estes números formam o conjunto dos números inteiros, indicado por ℤ.
Não pertencem aos números inteiros: as frações, números decimais, os números irracionais e os complexos.
O conjunto dos números inteiros é infinito e pode ser representado da seguinte maneira:
ℤ = {…-6, -5, -4, – 3, – 2, – 1, 0, 1, 2, 3,4 ,5 ,6 …}
Os números inteiros negativos são sempre acompanhados pelo sinal (-), enquanto os números inteiros positivos podem vir ou não acompanhados de sinal (+).
O zero é um número neutro, ou seja, não é um número nem positivo e nem negativo.
A relação de inclusão no conjunto dos inteiros envolve o conjunto dos números naturais (ℕ).
Todo número inteiro possui um antecessor e um sucessor. Por exemplo, o antecessor de -2 é -3, já o seu sucessor é o -1.
Representação na Reta Numérica
Os números inteiros podem ser representados por pontos na reta numérica. Nesta representação, a distância entre dois números consecutivos é sempre a mesma.
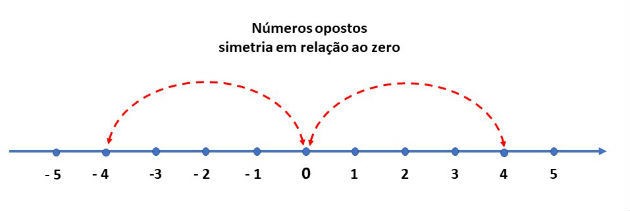
Os números que estão a uma mesma distância do zero, são chamados de opostos ou simétricos.
Por exemplo, o -4 é o simétrico de 4, pois estão a uma mesma distância do zero, conforme assinalado na figura abaixo:
Subconjuntos de ℤ
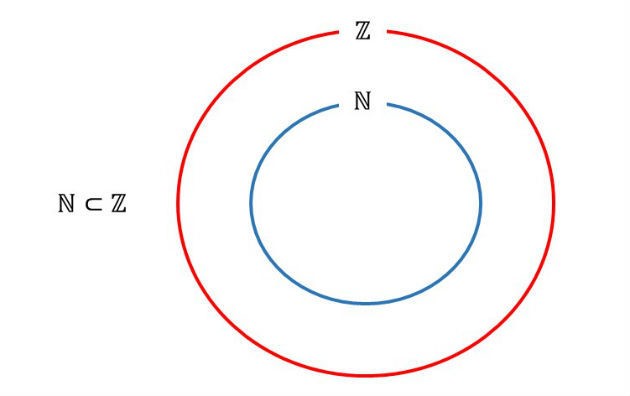
O conjunto dos números naturais (ℕ) é um subconjunto de ℤ, pois está contido no conjunto dos números inteiros. Assim:
Além do conjunto dos números naturais, destacamos os seguintes subconjuntos de ℤ:
- ℤ* : é o subconjunto dos números inteiros, com exceção do zero.
ℤ* = {…, -3,-2,-1, 1, 2, 3, 4, …}
- ℤ+ : são os números inteiros não-negativos, ou seja
ℤ+ = {0, 1, 2, 3, 4, …}
- ℤ _ : é o subconjunto dos números inteiros não-positivos, ou seja
ℤ_= {…, -4,-3,-2,-1, 0}
- ℤ*+ : é o subconjunto dos números inteiros, com exceção dos negativos e do zero.
ℤ*+ = {1,2,3,4, 5…}
- ℤ*_ : são os números inteiros, com exceção dos positivos e do zero, ou seja ℤ*_= {…, -4,-3,-2,-1}
Comparação entre números inteiros
Comparar dois números significa dizer se o primeiro é maior do que (>), menor do que (<) o igual ao (=) segundo número.
Exemplo 1: +245 > + 186 ; +96 < +102
Exemplo 2: +53 > 0 ; 0 < +38
Exemplo 3: – 25 < 0 ; 0 > -18
Exemplo 4: +25 > -19 ; -64 < +18.
Exemplo 5: -34 < -19 ; -6 > -12 ; -9 > -15
Exercícios
1) Indique o antecessor e o sucessor dos seguintes números:
a) -34
b) -8
c) 0
2) Determine o oposto (ou simétrico) dos seguintes números:
a) 9
b) -3
c) -145
d) 98
3) Construa uma reta numérica e destaque os números: 2, -3, -1, 4, -4.
4) Observe os números e diga:
-15, +6, -1, 0, +54, +12, -93, -8, +23, -72, +72
a) Quais os números inteiros negativos?
b) Quais são os números inteiros positivos?
c) Qual o número inteiro que não é nem positivo nem negativo?
5) Quais das seguintes sentenças são verdadeiras?
a) +4 = 4 = ( )
b) -6 = 6 = ( )
c) -8 = 8 = ( )
d) 54 = +54 = ( )
e) 93 = -93 = ( )
6) As temperaturas acima de 0°C (zero grau) são representadas por números positivos e as temperaturas abaixo de 0°C, por números negativos. Represente a seguinte situação com números inteiros:
a) 5° acima de zero =
b) 3° abaixo de zero =
c) 9°C abaixo de zero=
d) 15° acima de zero =
7) Determine:
a) O oposto de +5 =
b) O oposto de -9 =
c) O oposto de +6 =
d) O oposto de -6 =
e) O oposto de +18 =
f) O oposto de -15 =
g) O oposto de +234=
h) O oposto de -1000 =
8) Coloque os números em ordem crescente.
a) -9, -3, -7, +1, 0
b) -2, -6, -5, -3, -8
c) 5, -3, 1, 0, -1, 20
d) 25, -3, -18, +15, +8, -9
e) +60, -21, -34, -105, -90
f) -400, +620, -840, +1000, -100
9) Coloque os números em ordem decrescente:
a) +3, -1, -6, +5, 0
b) -4, 0, +4, +6, -2
c) -5, 1, -3, 4, 8
d) +10, +6, -3, -4, -9, +1
e) -18, +83, 0, -172, -64
f) -286, -740, +827, 0, +904

excelente essa vídeo aula
Na 4 (c)=0
Ótima aula!
Ótima aula
Preciso estagiar matemática na sexta série. Não estou segura
*
Muito bom
ヾ(≧▽≦*)o
to penando mais estou conseguindo
muito bom, perfeito
Ótima aula.
esta um pouco difícil mais estou conseguindo realizar.
Amei
eu gostei da sua aula o senhor explica super bem
amanha eu vo ter uma prova de matematica e essa aula ajudou muito entao muito obrigado;\
boa explicaçao melhor do que dasescola