Matemática 1ª série Ensino Médio
-
10.1 Conjuntos2 Tópicos|2 Questionários
-
10.2 Funções5 Tópicos|4 Questionários
-
10.3 Função Afim4 Tópicos|4 Questionários
-
10.4 Função Quadrática5 Tópicos|5 Questionários
-
10.5 Função Modular3 Tópicos|3 Questionários
-
10.6 Função Exponencial6 Tópicos|6 Questionários
-
10.7 Função Logarítmica7 Tópicos|7 Questionários
-
10.8 Tipos de Funções3 Tópicos|3 Questionários
-
10.9 Semelhanças1 Tópico|1 Questionário
-
10.10 Triângulos3 Tópicos|3 Questionários
-
10.11 Razões Trigonométricas2 Tópicos|2 Questionários
-
10.12 Triângulos1 Tópico|1 Questionário
-
10.13 Polígonos1 Tópico|1 Questionário
-
10.14 Circunferência e Círculo2 Tópicos|2 Questionários
-
10.15 Sequências1 Tópico|1 Questionário
-
10.16 Progressões Aritméticas PA2 Tópicos|2 Questionários
-
10.17 Progressões Geométricas PG4 Tópicos|4 Questionários
-
10.18 Matemática Financeira4 Tópicos|4 Questionários
-
10.19 Vetores2 Tópicos|2 Questionários
Conjuntos numéricos
Conjuntos Numéricos
Os conjuntos numéricos reúnem diversos conjuntos cujos elementos são números. Eles são formados pelos números naturais, inteiros, racionais, irracionais e reais.
Conjunto dos Números Naturais (N)
O conjunto dos números naturais é representado por N. Ele reúne os números que usamos para contar (incluindo o zero) e é infinito.
Subconjuntos dos Números Naturais
- N* = {1, 2, 3, 4, 5…, n, …} ou N* = N – {0}: conjuntos dos números naturais não-nulos, ou seja, sem o zero.
- Np = {0, 2, 4, 6, 8…, 2n, …}, em que n ∈ N: conjunto dos números naturais pares.
- Ni = {1, 3, 5, 7, 9…, 2n+1, …}, em que n ∈ N: conjunto dos números naturais ímpares.
- P = {2, 3, 5, 7, 11, 13, …}: conjunto dos números naturais primos.
Conjunto dos Números Inteiros (Z)
O conjunto dos números inteiros é representado por Z. Reúne todos os elementos dos números naturais (N) e seus opostos. Assim, conclui-se que N é um subconjunto de Z (N ⊂ Z):
Subconjuntos dos Números Inteiros
- Z* = {…, –4, –3, –2, –1, 1, 2, 3, 4, …} ou Z* = Z – {0}: conjuntos dos números inteiros não-nulos, ou seja, sem o zero.
- Z+ = {0, 1, 2, 3, 4, 5, …}: conjunto dos números inteiros e não-negativos. Note que Z+ = N.
- Z*+ = {1, 2, 3, 4, 5, …}: conjunto dos números inteiros positivos e sem o zero.
- Z – = {…, –5, –4, –3, –2, –1, 0}: conjunto dos números inteiros não-positivos.
- Z*– = {…, –5, –4, –3, –2, –1}: conjunto dos números inteiros negativos e sem o zero.
Conjunto dos Números Racionais (Q)
O conjunto dos números racionais é representado por Q. Reúne todos os números que podem ser escritos na forma p/q, sendo p e q números inteiros e q≠0.
Q = {0, ±1, ±1/2, ±1/3, …, ±2, ±2/3, ±2/5, …, ±3, ±3/2, ±3/4, …}
Note que todo número inteiro é também número racional. Assim, Z é um subconjunto de Q.
Importante ressaltar que as dízimas periódicas são números racionais. Elas são números decimais que se repetem após a vírgula, por exemplo: 1,4444444444… Embora possua infinitas casas decimais, pode ser escrito como a fração 13/9.
Subconjuntos dos Números Racionais
- Q* = subconjunto dos números racionais não-nulos, formado pelos números racionais sem o zero.
- Q+ = subconjunto dos números racionais não-negativos, formado pelos números racionais positivos e o zero.
- Q*+ = subconjunto dos números racionais positivos, formado pelos números racionais positivos, sem o zero.
- Q– = subconjunto dos números racionais não-positivos, formado pelos números racionais negativos e o zero.
- Q*– = subconjunto dos números racionais negativos, formado números racionais negativos, sem o zero.
Conjunto dos Números Irracionais (I)
O conjunto dos números irracionais é representado por I. Reúne os números decimais não exatos com uma representação infinita e não periódica, por exemplo: 3,141592… ou 1,203040…
Conjunto dos Números Reais (R)
O conjunto dos números reais é representado por R. Esse conjunto é formado pelos números racionais (Q) e irracionais (I). Assim, temos que R = Q ∪ I. Além disso, N, Z, Q e I são subconjuntos de R.
Mas, observe que se um número real é racional, ele não pode ser também irracional. Da mesma maneira, se ele é irracional, não é racional.
Subconjuntos dos Números Reais
- R*= {x ∈ R│x ≠ 0}: conjunto dos números reais não-nulos.
- R+ = {x ∈ R│x ≥ 0}: conjunto dos números reais não-negativos.
- R*+ = {x ∈ R│x > 0}: conjunto dos números reais positivos.
- R– = {x ∈ R│x ≤ 0}: conjunto dos números reais não-positivos.
- R*– = {x ∈ R│x < 0}: conjunto dos números reais negativos.
Intervalos Numéricos
Há ainda um subconjunto relacionado com os números reais que são chamados de intervalos. Sejam a e b números reais e a < b, temos os seguintes intervalos reais:
Intervalo aberto de extremos: ]a,b[ = {x ∈ R│a < x < b}

Intervalo fechado de extremos: [a,b] = {x ∈ R│a ≤ x ≤ b}

Intervalo aberto à direta (ou fechado à esquerda) de extremos: [a,b[ = {x ∈ R│a ≤ x < b}

Intervalo aberto à esquerda (ou fechado à direita) de extremos: ]a,b] = {x ∈ R│a < x ≤ b}

Propriedades dos Conjuntos Numéricos
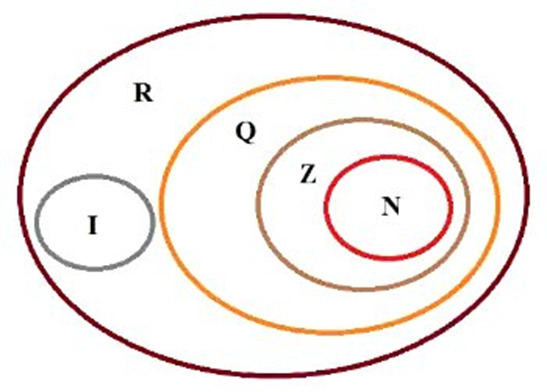
Diagrama dos conjuntos numéricos
Para facilitar os estudos sobre os conjuntos numéricos, segue abaixo algumas de suas propriedades:
- O conjunto dos números naturais (N) é um subconjunto dos números inteiros: Z (N ⊂ Z).
- O conjunto dos números inteiros (Z) é um subconjunto dos números racionais: (Z ⊂ Q).
- O conjunto dos números racionais (Q) é um subconjunto dos números reais (R).
- Os conjuntos dos números naturais (N), inteiros (Z), racionais (Q) e irracionais (I) são subconjuntos dos números reais (R).
Exercícios
1) Sejam a=|−8|, b= -6 e c=|5|. Calcule:
a) a+b
b) b ⋅ c
c) c-a
d) a ⋅ b+c
2) Diga se é verdadeira ou falsa cada proposição abaixo:
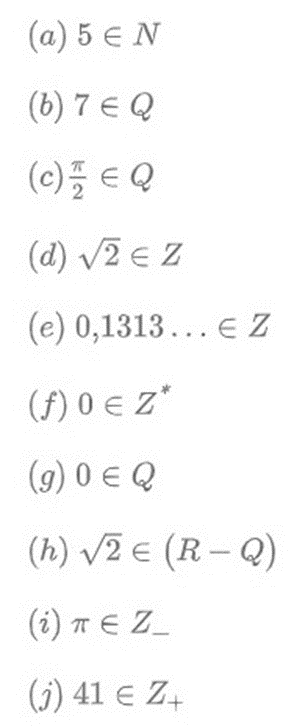
3) marque a(s) sentença(s) que apresenta(m) números irracionais:
a) √50
b) √72
c) 1+2π
d) (3–√+1)2
4) Sobre os conjuntos numéricos, marque a alternativa incorreta.
A) Todo número natural é também um número racional.
B) Um número racional não pode ser irracional.
C) Todo número negativo é um número inteiro.
D) O conjunto dos números reais é formado pela união dos números racionais e irracionais.
E) As dízimas periódicas são consideradas números racionais, portanto são também números reais.

adorei o conteúdo