Matemática 1ª série Ensino Médio
-
10.1 Conjuntos2 Tópicos|2 Questionários
-
10.2 Funções5 Tópicos|4 Questionários
-
10.3 Função Afim4 Tópicos|4 Questionários
-
10.4 Função Quadrática5 Tópicos|5 Questionários
-
10.5 Função Modular3 Tópicos|3 Questionários
-
10.6 Função Exponencial6 Tópicos|6 Questionários
-
10.7 Função Logarítmica7 Tópicos|7 Questionários
-
10.8 Tipos de Funções3 Tópicos|3 Questionários
-
10.9 Semelhanças1 Tópico|1 Questionário
-
10.10 Triângulos3 Tópicos|3 Questionários
-
10.11 Razões Trigonométricas2 Tópicos|2 Questionários
-
10.12 Triângulos1 Tópico|1 Questionário
-
10.13 Polígonos1 Tópico|1 Questionário
-
10.14 Circunferência e Círculo2 Tópicos|2 Questionários
-
10.15 Sequências1 Tópico|1 Questionário
-
10.16 Progressões Aritméticas PA2 Tópicos|2 Questionários
-
10.17 Progressões Geométricas PG4 Tópicos|4 Questionários
-
10.18 Matemática Financeira4 Tópicos|4 Questionários
-
10.19 Vetores2 Tópicos|2 Questionários
Definição de função 1ª série
Definição de Função.
Função é uma regra que relaciona cada elemento de um conjunto (representado pela variável x) a um único elemento de outro conjunto (representado pela variável y). Para cada valor de x, podemos determinar um valor de y, dizemos então que “y está em função de x”
Vamos representar uma função de números naturais de forma que, para cada número natural escolhido, obtenha-se o seu dobro. Por exemplo, se escolhermos o 1, teremos o número 2; se escolhermos o 2, teremos o 4; se escolhermos o 3, teremos o 6 e assim por diante. Podemos representar uma função utilizando o diagrama de flechas ou o diagrama de setas, como na figura a seguir:
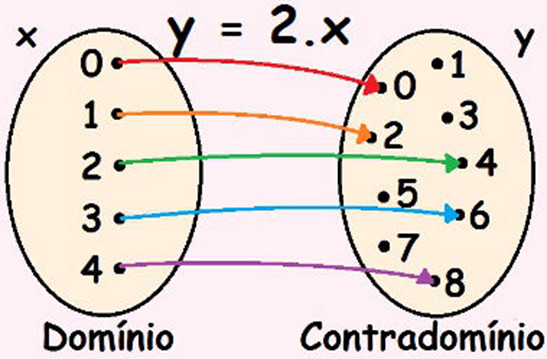
Nessa representação há dois conjuntos numéricos, um domínio e um contradomínio. Dentro do contradomínio há um subconjunto chamado de imagem. Esse subconjunto é composto pelos elementos que estão recebendo a seta, isto é, aqueles que possuem alguma relação com os elementos do domínio. Ao trabalharmos com funções, sempre teremos uma “lei da função” que determinará como serão os elementos da imagem dessa função. Nesse caso, há uma função de y em relação a x, uma vez que, para cada x escolhido, há um y. Dizemos ainda que y é a variável dependente e, por sua vez, que x é a variável independente.
Se os elementos do domínio e da imagem de uma função pertencem ao conjunto dos números inteiros, por exemplo, dizemos que f: Z→Z , lemos que “f é uma função cujo domínio pertence aos inteiros e cuja imagem pertence aos inteiros” ou, simplesmente, “f é uma função de inteiros em inteiros”.
Exemplo: observe os conjuntos A = {1, 2, 3, 4} e B = {1, 2, 3, 4, 5, 6, 7, 8}, com a função que determina a relação entre os elementos f: A → B é x → 2x. Sendo assim, f(x) = 2x e cada x do conjunto A é transformado em 2x no conjunto B.
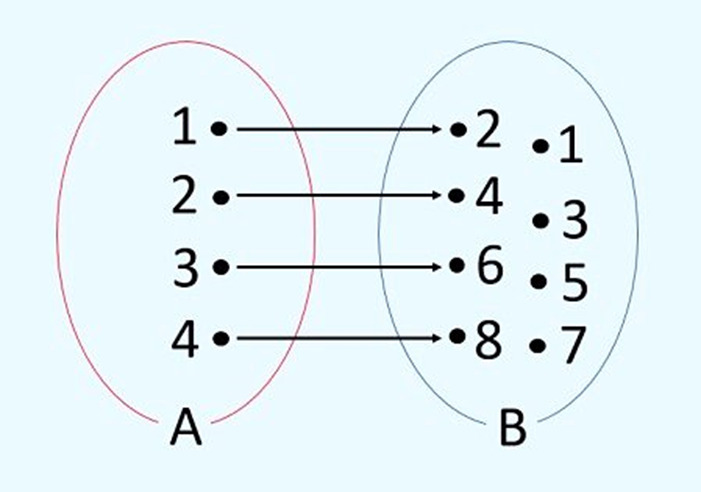
Note que o conjunto de A {1, 2, 3, 4} são as entradas, “multiplicar por 2” é a função e os valores de B {2, 4, 6, 8}, que se ligam aos elementos de A, são os valores de saída.
Portanto, para essa função:
- O domínio é {1, 2, 3, 4}
- O contradomínio é {1, 2, 3, 4, 5, 6, 7, 8}
- O conjunto imagem é {2, 4, 6, 8}
Exemplo
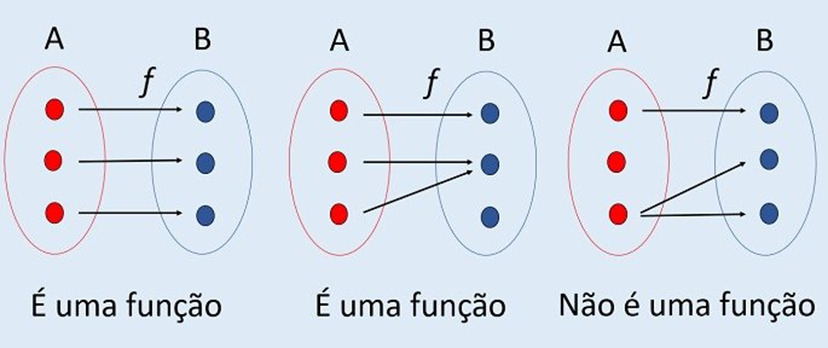
Notação para função: f: A → B (lê-se: f de A em B).
Tipos de funções
As funções recebem classificações de acordo com suas propriedades. Confira a seguir os principais tipos.
Função sobrejetora
Na função sobrejetora o contradomínio é igual ao conjunto imagem. Portanto, todo elemento de B é imagem de pelo menos um elemento de A.
Notação: f: A → B, ocorre a Im(f) = B
Exemplo:
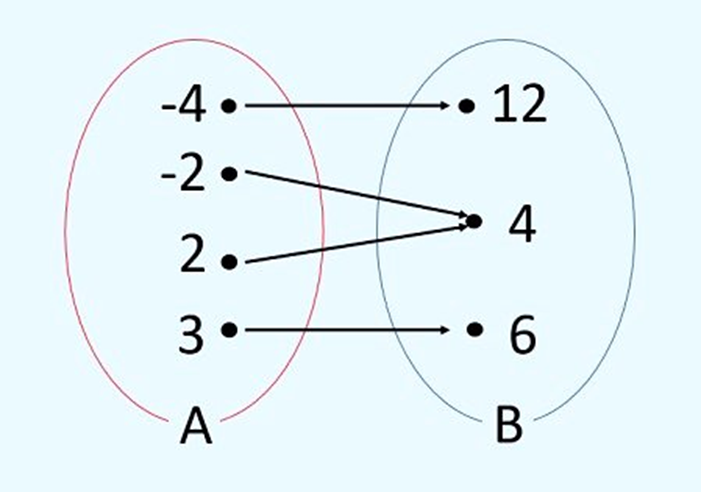
Para a função acima:
- O domínio é {-4, -2, 2, 3}
- O contradomínio é {12, 4, 6}
- O conjunto imagem é {12, 4, 6}
Função injetora
Na função injetora todos os elementos de A possuem correspondentes distintos em B e nenhum dos elementos de A compartilham de uma mesma imagem em B. Entretanto, podem existir elementos em B que não estejam relacionados a nenhum elemento de A.
Exemplo:
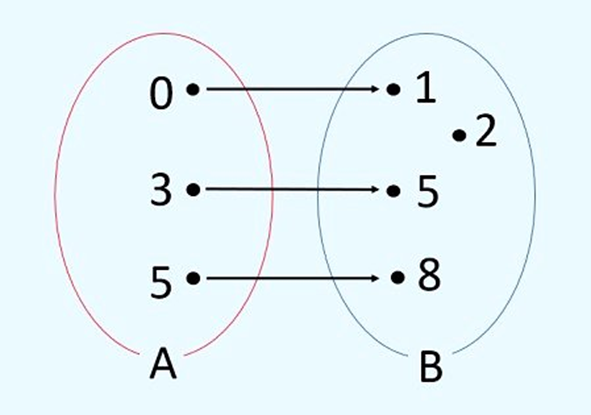
Para a função acima:
- O domínio é {0, 3, 5}
- O contradomínio é {1, 2, 5, 8}
- O conjunto imagem é {1, 5, 8}
Função bijetora
Na função bijetora os conjuntos apresentam o mesmo número de elementos relacionados. Essa função recebe esse nome por ser ao mesmo tempo injetora e sobrejetora.
Exemplo:
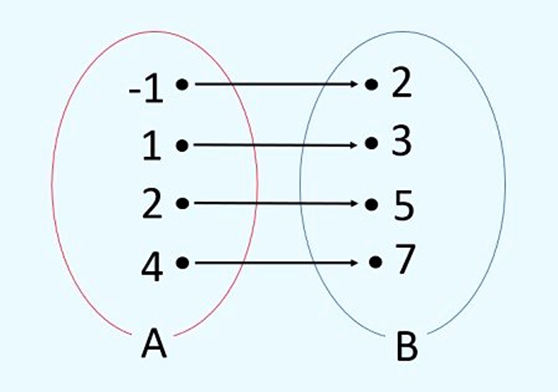
Para a função acima:
- O domínio é {-1, 1, 2, 4}
- O contradomínio é {2, 3, 5, 7}
- O conjunto imagem é {2, 3, 5, 7}
Exercícios
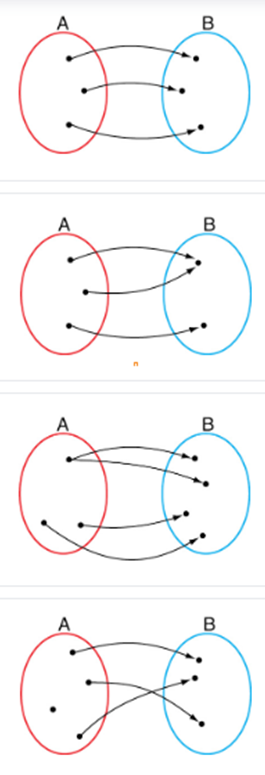
1) Marque somente a(s) alternativa(s) onde a relação representada no esquema é uma função de A em B. Considere que os pontos assinalados representam os elementos dos conjuntos A e B.
2) Sendo A={−1,0,1,2} e B={−2,−1,0,1,2,3,4}, marque a(s) alternativa(s) onde a lei dada define uma função de A com valores em B:
f(x)=2x
f(x)=x2
f(x)=2x+1
f(x)=|x|−1
3) Considere f uma função de R em R dada por f(x)=3x2 – x + 4. Calcule:
a) f(1)
b) f(-1)
c) f(0)
d)f(12)
4) Sendo f: F Q F dada por f(x)=2x+(−1)x, calcule:
a) f(0)
b) f(1)
c) f(2)
5) Uma função f: H Q H é definida pela lei f(x)=m⋅4x, sendo m uma constante real. Sabendo que f(1)=12, determine o valor de:
a) m
b) f(2)

Respostas