Matemática 1ª série Ensino Médio
-
10.1 Conjuntos2 Tópicos|2 Questionários
-
10.2 Funções5 Tópicos|4 Questionários
-
10.3 Função Afim4 Tópicos|4 Questionários
-
10.4 Função Quadrática5 Tópicos|5 Questionários
-
10.5 Função Modular3 Tópicos|3 Questionários
-
10.6 Função Exponencial6 Tópicos|6 Questionários
-
10.7 Função Logarítmica7 Tópicos|7 Questionários
-
10.8 Tipos de Funções3 Tópicos|3 Questionários
-
10.9 Semelhanças1 Tópico|1 Questionário
-
10.10 Triângulos3 Tópicos|3 Questionários
-
10.11 Razões Trigonométricas2 Tópicos|2 Questionários
-
10.12 Triângulos1 Tópico|1 Questionário
-
10.13 Polígonos1 Tópico|1 Questionário
-
10.14 Circunferência e Círculo2 Tópicos|2 Questionários
-
10.15 Sequências1 Tópico|1 Questionário
-
10.16 Progressões Aritméticas PA2 Tópicos|2 Questionários
-
10.17 Progressões Geométricas PG4 Tópicos|4 Questionários
-
10.18 Matemática Financeira4 Tópicos|4 Questionários
-
10.19 Vetores2 Tópicos|2 Questionários
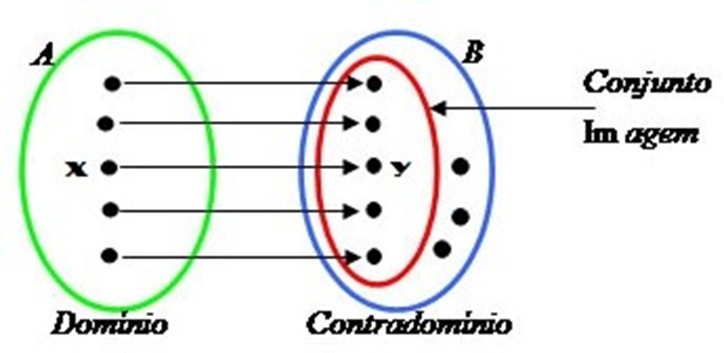
Domínio, contradomínio e imagem 1ª série
Domínio Contradomínio e Imagem
Uma função é uma regra que relaciona cada elemento de um conjunto A a um único elemento de um conjunto B. De acordo com essa definição, as funções necessariamente devem relacionar todos os elementos do primeiro conjunto, mas nem todos os elementos do segundo conjunto serão “usados”. São nesses dois conjuntos que podemos encontrar o domínio, o contradomínio e a imagem de uma função.
Algebricamente, uma função é definida da seguinte maneira:
f: A → B
y = f(x)
Em que f é a letra escolhida para representar a função, e y = f(x) é a regra da função.
O símbolo A → B quer dizer que os elementos do conjunto A serão avaliados na regra f(x) e terão como resultado um elemento do conjunto B. A letra x, em uma função, representa um elemento qualquer do conjunto A, por isso, é chamada de variável: pode assumir qualquer valor, desde que esse valor seja um dos elementos de A.
Além disso, x também é variável independente, pois é essa variável que determina qual elemento do conjunto B será relacionado ao elemento do conjunto A por meio da regra y = f(x).
A variável y é dependente da variável x, por essa razão, é nomeada como variável dependente. Em resumo, a variável x representa um elemento qualquer do conjunto A, e a variável y refere-se a um elemento qualquer do conjunto B.
O que é domínio, contradomínio e imagem?
Dada a função y = f(x) que relaciona os elementos do conjunto A aos elementos do conjunto B, podemos definir:
1 – O conjunto A é conhecido como domínio. Esse nome é escolhido para esse conjunto devido ao papel dos seus elementos na função. Lembre-se de que o conjunto A é que determina a variável independente. Portanto, os elementos do conjunto A possuem o “domínio” sobre os resultados da função, uma vez que os resultados de y obtidos dependem do valor x escolhido.
Exemplo – dada a função:
f: N → Z
y = 2x
O conjunto dos naturais é o domínio, portanto, os números que poderão ser relacionados estão no conjunto:
N = {0, 1, 2, 3, 4, 5, 6, 7, …}
2 – O conjunto B é conhecido como contradomínio. Esse nome é escolhido pelo fato de que nem todos os elementos do conjunto B precisam ser usados para que a função seja válida. Além disso, esse nome remete à dependência que existe entre os conjuntos A e B.
O contradomínio é o conjunto em que encontraremos todos os números que podem ser relacionados aos elementos do domínio por meio da função f. Tomando novamente o exemplo anterior:
f: N → Z
y = 2x
O contradomínio é o conjunto formado por todos os números inteiros. Note que alguns números inteiros nunca poderão ser resultados de uma multiplicação de um número natural por 2, como o número 7. Assim, embora o número 7 pertença ao contradomínio, ele não pode ser relacionado a nenhum número no domínio.
3 – O subconjunto do contradomínio, formado por todos os seus elementos que se relacionam a algum elemento do domínio, é denominado de imagem.
Assim, na função anterior:
f: N → Z
y = 2x
Embora o conjunto de todos os números inteiros seja o contradomínio dessa função, apenas os números pares serão resultados de algum elemento do domínio aplicado na regra da função. Portanto, o conjunto imagem dessa função é o conjunto dos números pares.
Exercícios
1) Sejam os conjuntos A={-2,-1,0,1,2} e B={-1,0,1,2,3,4,5}. Em cada caso, determine o domínio, o contradomínio e o conjunto imagem de f.
a) f: A→B
dada por
f(x)=x+2
b) f: A→B
dada por
f(x)=x+2
c) f: A→B
dada por
f(x)=x+2
d) f: A→B
dada por
f(x)=x+2
2) Se A={x∈Z|−2≤x≤2} e B={x∈Z|−5≤x≤5}e f: A→B é definida pela lei y=2x+1, quantos são os elementos de B que não pertencem ao conjunto imagem da função?
3)Se x e y são números reais, estabeleça o domínio de cada uma das funções dadas pelas leis a seguir.
R – {1} R R R*
y= − 4x2 + 3x − 1
y= (−3x+11) / 2
y= (2x + 3) / x
y= 4 / x − 1

Respostas