Matemática 1ª série Ensino Médio
-
10.1 Conjuntos2 Tópicos|2 Questionários
-
10.2 Funções5 Tópicos|4 Questionários
-
10.3 Função Afim4 Tópicos|4 Questionários
-
10.4 Função Quadrática5 Tópicos|5 Questionários
-
10.5 Função Modular3 Tópicos|3 Questionários
-
10.6 Função Exponencial6 Tópicos|6 Questionários
-
10.7 Função Logarítmica7 Tópicos|7 Questionários
-
10.8 Tipos de Funções3 Tópicos|3 Questionários
-
10.9 Semelhanças1 Tópico|1 Questionário
-
10.10 Triângulos3 Tópicos|3 Questionários
-
10.11 Razões Trigonométricas2 Tópicos|2 Questionários
-
10.12 Triângulos1 Tópico|1 Questionário
-
10.13 Polígonos1 Tópico|1 Questionário
-
10.14 Circunferência e Círculo2 Tópicos|2 Questionários
-
10.15 Sequências1 Tópico|1 Questionário
-
10.16 Progressões Aritméticas PA2 Tópicos|2 Questionários
-
10.17 Progressões Geométricas PG4 Tópicos|4 Questionários
-
10.18 Matemática Financeira4 Tópicos|4 Questionários
-
10.19 Vetores2 Tópicos|2 Questionários
Taxa média de variação de uma função 1ª série
Taxa de variação média
A taxa de variação média da função f no intervalo [a,b], é dada pela expressão:
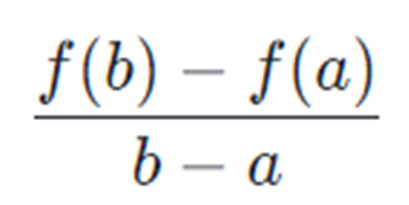
É uma medida de quanto a função mudou por unidade, em média, nesse intervalo.
Ela deriva do coeficiente angular da linha reta que liga as extremidades do intervalo no gráfico da função.
Cálculo da taxa de variação média
Exemplo 1: Taxa de variação média a partir do gráfico
Vamos calcular a taxa de variação média de f no intervalo [0, 9]:

É possível ver, no gráfico, que f(0)=-7 e f(9)=3
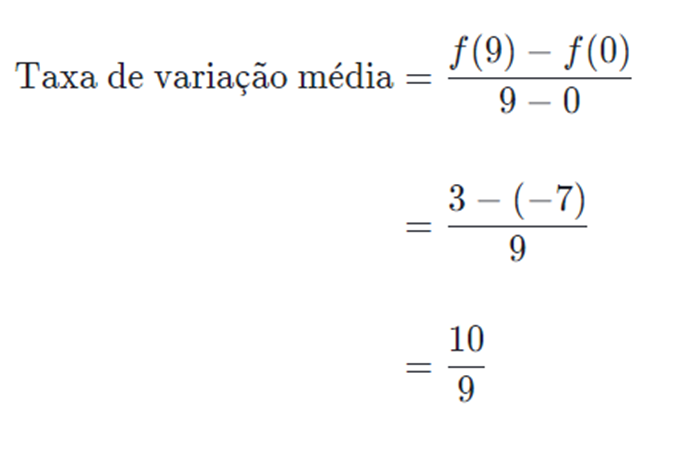
Exemplo 2: Taxa de variação média a partir da equação
Vamos calcular a taxa de variação média de g(x)= x3 – 9x no intervalo [1,6].
g(1)=13-9.1=-8
g(6)=63-9.6=162
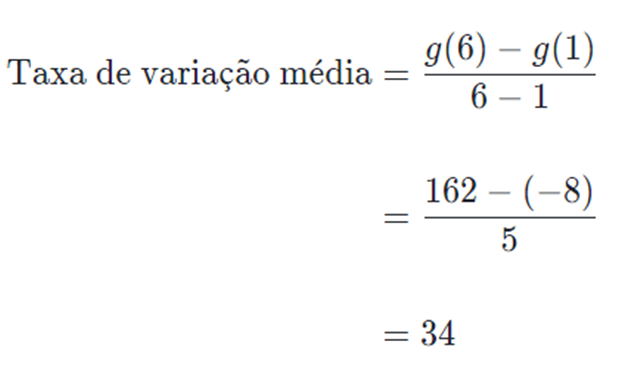
Exercícios
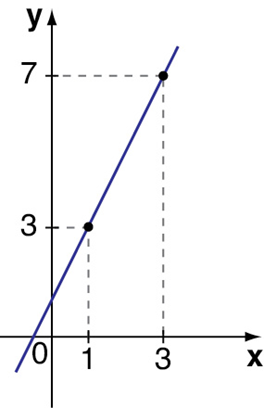
1) Calcule a taxa média de variação da função cujo gráfico está representado, quando x varia de 1 a 3:
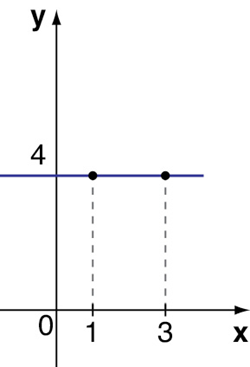
2) Calcule a taxa média de variação da função cujo gráfico está representado, quando x varia de 1 a 3:
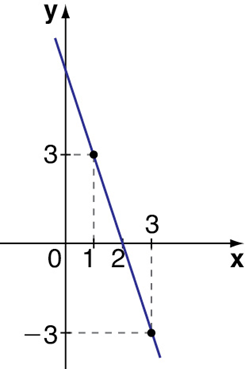
3) Calcule a taxa média de variação da função cujo gráfico está representado, quando x varia de 1 a 3:
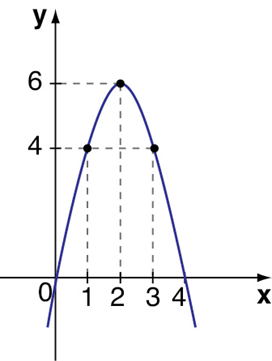
4) Calcule a taxa média de variação da função cujo gráfico está representado, quando x varia de 1 a 3:
Taxa de variação média
A taxa de variação média da função f no intervalo [a,b], é dada pela expressão:

Respostas