Provas de Matematica OBMEP 2012 – Nivel 2
[adinserter block=”1″]
Este Simulado de matemática possui todas questões da Prova de Matematica OBMEP 2012 – Nivel 2.
Ao final você receberá sua nota.
Separe uma folha de rascunho e um lápis para fazer os cálculos.
Para ter uma experiência única, CADASTRE-SE GRATUITAMENTE e receba em seu email todos os materiais exclusivos grátis do site.
CLIQUE NO BOTÃO ABAIXO para começar. Boa prova! ?
?
Teste de Razões trigonométricas Matemática 2ª série
Teste de Razões trigonométricas Matemática 2ª série online. Ao final receba a sua nota. Conquiste os desafios!
Teste Summary
0 of 24 Perguntas completed
Perguntas:
Information
Você já concluiu o teste antes. Portanto, você não pode reiniciá-lo.
Teste is loading...
You must sign in or sign up to start the teste.
Você precisa primeiro terminar o seguinte:
Resultados
Resultados
0 of 24 Perguntas answered correctly
Seu tempo:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Pontos Médios |
|
| Sua pontuação |
|
Categories
- Not categorized 0%
-
Você precisa melhorar! Você acertou menos que 70% das questões Tente novamente!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Muito bom, Você acertou mais que 70% das questões, você passou!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Parabéns! Você acertou mais que 90% das questões. Siga para os próximos exercícios!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
| Pos. | Nome | Entered on | Pontos | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- Current
- Review
- Answered
- Correto
- Incorreto
-
Question 1 of 24
1. Question
(UFSJ-MG) Considerando os valores de \(\theta\), para os quais a expressão \(\frac { sen\theta }{ cossec\theta }\) + \(\frac { cos\theta }{ sec\theta }\) é definida, é correto afirmar que ela está sempre igual a:
CorretoIncorreto -
Question 2 of 24
2. Question
(Uern) Considerando que \({ sen }^{ 2 }\alpha =\frac { 3 }{ 4 }\), com 0° < \(\alpha\) < 90°, então o valor da expressão \(\left( cos\frac { \alpha }{ 2 } +sen\alpha \right) . tg\alpha \)é
CorretoIncorreto -
Question 3 of 24
3. Question
(EsPCEx-SP) O valor de (cos 165° + sen 155° + cos 145° - sen 25° + cos 35° + cos 15°) é
CorretoIncorreto -
Question 4 of 24
4. Question
(FGV-SP) Sabendo que o valor da secante de x é dado por sec x = \(\frac { 5 }{ 4 }\), em que x pertence ao intervalo \(\left[ \frac { 3\pi }{ 2 } , 2\pi \right]\), podemos afirmar que os valores de cos x, sen x e tg x são respectivamente:
CorretoIncorreto -
Question 5 of 24
5. Question
(Uece) Se x é um arco localizado no segundo quadrante e cos x = -\(\frac { 3 }{ 5 }\), entãol o valor de cos x + sen x + tg x + cotg x + sec x + cossec x é:
CorretoIncorreto -
Question 6 of 24
6. Question
(PUC-RJ) Se tg \(\theta\) = 1 e \(\theta\) pertence ao primeiro quadrante, então cos \(\theta\) é igual a:
CorretoIncorreto -
Question 7 of 24
7. Question
(FEI-SP) Simplificando a expressão \(\sqrt { 1 + { cotg }^{ 2 } x } }{ 3 { sec }^{ 2 } }\) onde existir, obtemos:
CorretoIncorreto -
Question 8 of 24
8. Question
(Cefet-PR) Considere as afirmações a seguir, em relação a razões trigonométricas no ciclo trigonométrico:
I. cotg \(\frac { \pi }{ 6 }\) = tg \(\frac { 4\pi }{ 3 }\)
II. sec 60° = sen 90° - cos 180°
III. sen 316° - cos 314°
IV. cossec 30° = sen 120°Somente estão corretas:
CorretoIncorreto -
Question 9 of 24
9. Question
(UFRR) Indique qual das afirmações abaixo é verdadeira:
CorretoIncorreto -
Question 10 of 24
10. Question
(UPE) Na figura ao lado, estão representados o ciclo trigonométrico e um triângulo trigonométrico e um triângulo isósceles OAB. Qual das expressões abaixo corresponde a área do triângulo OAB em função do ângulo \(\alpha\)
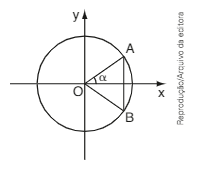 CorretoIncorreto
CorretoIncorreto -
Question 11 of 24
11. Question
(UEG-GO) Sabendo-se que sen(x) = \(\)\frac { 1 }{ 2 } e que x é um ângulo do 1º quadrante, o valor da expressão sen (4x) - cos (4x) é
CorretoIncorreto -
Question 12 of 24
12. Question
(Unicamp-SP) Seja x real tal que cos x = tg x. O valor de sen x é:
CorretoIncorreto -
Question 13 of 24
13. Question
(Unesp-SP) Dada a expressão f(x) = \(\log _{ 10 }\left[ \frac { 1 }{ sen(x).cossec (x) } \right], com x \in R\) pode-se afirmar que:
CorretoIncorreto -
Question 14 of 24
14. Question
(Mack-SP) O maior valor que o número real [\(\frac { 10 }{ 2 - \frac { senx }{ 3 } } \) pode assumir é
CorretoIncorreto -
Question 15 of 24
15. Question
(Insper-SP) O professor de Matemática de Artur e Bia pediu aos alunos que colocassem suas calculadoras científicas no modo "radianos" e calculassem o valor de sen \(\frac { \pi }{ 2 }\). Tomando um valor aproximado, Artur digitou em sua calculadora o número 1,6 e, em seguida, calculou o seu seno, encontrando o valor A. Bia calculou o seno de 1,5, obtendo o valor B. Considerando que \(\frac { \pi }{ 2 }\) vale aproximadamente 1,5708, assinale a alternativa que traz a correta ordenação dos valores A, B e sen \(\frac { \pi }{ 2 }\).
CorretoIncorreto -
Question 16 of 24
16. Question
(Cefet-MG) Considerando-se a soma
S = \(\left[ \frac { \pi }{ 2 } +\frac { \pi }{ 6 } +\frac { \pi }{ 18 } +\frac { \pi }{ 54 } \right] \), o valor de cos(S) é igual a:CorretoIncorreto -
Question 17 of 24
17. Question
(FGV-SP) No círculo trigonométrico de raio unitário indicado na figura, o arco \(\bar { AB } mede \alpha\). Assim, PM é igual a:
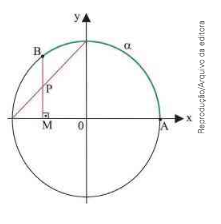 CorretoIncorreto
CorretoIncorreto -
Question 18 of 24
18. Question
(Enem) Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d \(\preceq\) r sobre a circunferência.
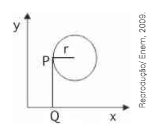
Então o ponto Q percorrerá, no eixo x, uma distância dada por:CorretoIncorreto -
Question 19 of 24
19. Question
(Fuvest-SP) Sabe-se que x = 1 é raiz da equação \(({ cos }^{ 2 }\alpha){ x }^{ 2 } - cos(4cos \alpha sen \beta)x +\frac { 3 }{ 2 } sen \beta = 0, sendo \alpha e \beta\) os ângulos agudos indicados no triângulo retângulo da figura abaixo.
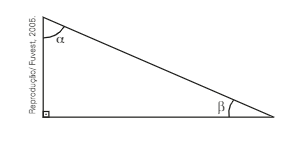
Pode-se então afirmar que as medidas de \(\alpha e \beta\) são, respectivamente:
CorretoIncorreto -
Question 20 of 24
20. Question
(Fuvest-SP) O dobro do seno de um ângulo \(\theta, 0 < \theta < \frac {\pi}{2}\), é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno é:
CorretoIncorreto -
Question 21 of 24
21. Question
(UEPB) Dados tg x = -2 e x um arco do 2º quadrante, o valor de sec x + cossec x é:
CorretoIncorreto -
Question 22 of 24
22. Question
(Unesp-SP) Se tg(x) = \(\frac { 2ab }{ { a}^{ 2 } - { b}^{ 2 } }\), em que a > b > 0 e 0° < x < 90°, então o valor de sen(x) é:
CorretoIncorreto -
Question 23 of 24
23. Question
(Fuvest-SP) O triângulo AOB é isósceles, com AO = OB, e ABCD é um quadrado. Sendo \(\theta\) a medida do ângulo AOB, pode-se garantir que a área d(Fuvest-SP) O triângulo AOB é isósceles, com AO = OB, e ABCD é um quadrado. Sendo \(\theta\) a medida do ângulo AOB, pode-se garantir que a área do quadrado é maior do que a área do triângulo se:o quadrado é maior do que a área do triângulo se:
 CorretoIncorreto
CorretoIncorreto -
Question 24 of 24
24. Question
(Ufam) Se
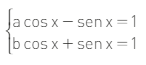 então o produto a . b é igual a:CorretoIncorreto
então o produto a . b é igual a:CorretoIncorreto
Resolva todas Provas da OBMEP
[vc_tta_tabs color=”orange” active_section=”1″][vc_tta_section title=”2015″ tab_id=”obmep-2015″][vc_column_text]Prova OBMEP 2015 – Nível 1
Prova OBMEP 2015 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2014″ tab_id=”obmep-2014″][vc_column_text]Prova OBMEP 2014 – Nível 1
Prova OBMEP 2014 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2013″ tab_id=”obmep-2013″][vc_column_text]Prova OBMEP 2013 – Nível 1
Prova OBMEP 2013 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2012″ tab_id=”obmep-2012″][vc_column_text]Prova OBMEP 2012 – Nível 1
Prova OBMEP 2012 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2011″ tab_id=”obmep-2011″][vc_column_text]Prova OBMEP 2011 – Nível 1
Prova OBMEP 2011 – Nível 3[/vc_column_text][/vc_tta_section][/vc_tta_tabs]
Pratique outros: Exercicios de Matematica.
Essas foram as questões da prova de matemática do exame da Olimpíada Brasileira de Matemática das Escolas Públicas – OBMEP de 2012, nível 2, ou seja, do 8º e 9º ano do ensino fundamental.
Neste simulado, você resolve a questão e confere a resposta correta com as videoaulas de resolução dos exercícios da equipe do OBMEP. Ao final você recebe sua nota e o desempenho em cada bloco de conteúdo da matemática.
Estude: Tudo sobre Matematica basica.
Aprenda matematica de forma simples e objetiva.
Cadastre-se gratuitamente no Matemática Zup!
E então, conferiu o gabarito? Como se saiu neste simulado de matemática?
Deixe o seu comentário, conversamos logo abaixo.
[wpseo_breadcrumb]

Responses