Provas de Matematica OBMEP 2014 – Nivel 2
Este Simulado de matemática possui todas questões da Prova de Matematica OBMEP 2014 – Nivel 2.
Ao final você receberá sua nota.
Separe uma folha de rascunho e um lápis para fazer os cálculos.
Para ter uma experiência única, CADASTRE-SE GRATUITAMENTE e receba em seu email todos os materiais exclusivos grátis do site.
CLIQUE NO BOTÃO ABAIXO para começar. Boa prova! ?
?
Teste de A reta Matemática 3ª série
Teste de A reta Matemática 3ª série online. Ao final receba a sua nota. Conquiste os desafios!
Teste Summary
0 of 42 Perguntas completed
Perguntas:
Information
Você já concluiu o teste antes. Portanto, você não pode reiniciá-lo.
Teste is loading...
You must sign in or sign up to start the teste.
Você precisa primeiro terminar o seguinte:
Resultados
Resultados
0 of 42 Perguntas answered correctly
Seu tempo:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Pontos Médios |
|
| Sua pontuação |
|
Categories
- Not categorized 0%
-
Você precisa melhorar! Você acertou menos que 70% das questões Tente novamente!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Muito bom, Você acertou mais que 70% das questões, você passou!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Parabéns! Você acertou mais que 90% das questões. Siga para os próximos exercícios!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
| Pos. | Nome | Entered on | Pontos | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- Current
- Review
- Answered
- Correto
- Incorreto
-
Question 1 of 42
1. Question
\(\left( UPE \right) \) No plano cartesiano, a reta s: 4x -3y +12 =0 intersecta o eixo das abscissas no ponto A e o eixo das ordenadas no ponto B . Nessas condições, qual é a distância entre os pontos A e B ?
CorretoIncorreto -
Question 2 of 42
2. Question
\(\left( Ufam \right) \) Considere as retas r:2y - x = 10 e s: y + 2x = 5.
É correto afirmar que:
CorretoIncorreto -
Question 3 of 42
3. Question
\(\left( UFPR \right) \) Considere a reta r de equação y = 2x + 1.
Qual das retas abaixo é perpendicular à reta r e passa pelo ponto P = \(\left( 4,2 \right) \) ?
CorretoIncorreto -
Question 4 of 42
4. Question
\(\left( UFRGS-RS\right) \) No pentágono representado abaixo no sistema de coordenadas cartesianas abaixo, os vértices possuem coordenadas inteiras.
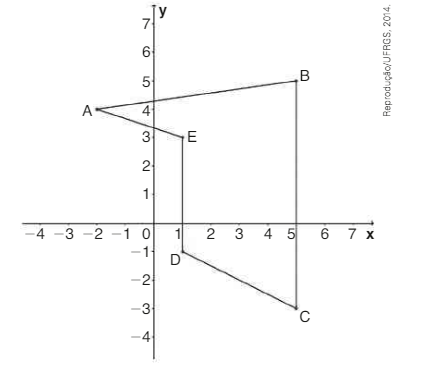
As retas suporte dos lados \( \bar {AE } \) e \( \bar {BC } \) intersectam-se no ponto:
CorretoIncorreto -
Question 5 of 42
5. Question
\( \left( Unicamp-SP \right) \) No plano cartesiano, a reta de equação 2x - 3y = 12 intersecta os eixos coordenados nos pontos A e B. O ponto médio dos segmentos \( \bar { AB} \) tem coordenadas:
CorretoIncorreto -
Question 6 of 42
6. Question
\( \left( UFRGS-RS \right) \) As equações das retas representadas no sistema de coordenadas cartesianas abaixo são 2x + y - 3 = 0, 5x - 4y - 8 = 0 e x - 3y + 3 = 0.
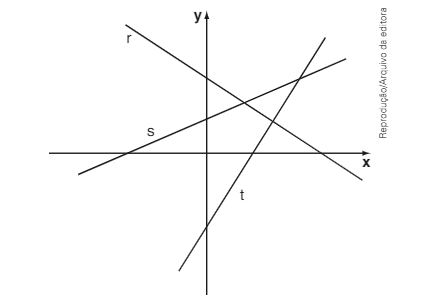
As equações de r e s são, respectivamente:
CorretoIncorreto -
Question 7 of 42
7. Question
\( \left( ITA-SP \right) \) A área do quadrilátero definido pelos eixos coordenados e as retas r: x - 3y + 3 = 0 e s: 3x + y - 21 = 0, em unidades de área, é igual a:
CorretoIncorreto -
Question 8 of 42
8. Question
\( \left( FGV-SP\right) \) No plano cartesiano, a reta \( \left( r\right)\) de equação y + kx = 2 é perpendicular á reta\( \left( s\right)\) que passa pela origem e pelo ponto \( \left( -5, 1\right)\) .
O ponto de interseção das retas \( \left( r\right)\) e \(\left( s\right)\) tem abscissa:
CorretoIncorreto -
Question 9 of 42
9. Question
\(\left( PUC-RJ\right) \) O triângulo ABC da figura abaixo tem área 25 e vértices A = \(\left( 4, 5 \right) \), B= \(\left( 4, 0 \right) \) e C = \(\left( c, 0 \right) \),
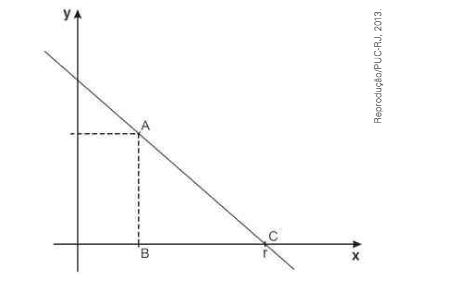
As equações de r e s são, respectivamente :
CorretoIncorreto -
Question 10 of 42
10. Question
\( \left(Ufscar- SP \right) \) O retângulo da figura tem como vértices os pontos \( \left(1, 3 \right) \) , \( \left(5, 3 \right) \) , \( \left(5, -2 \right) \) e \( \left(1, -2 \right) \)
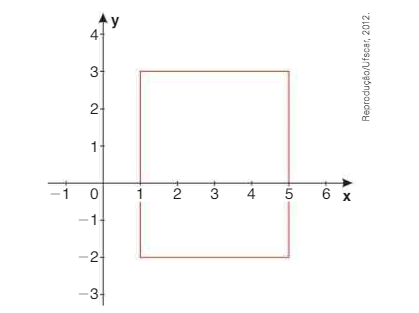
A equação da reta que passa pelo ponto \( \left(2, 0 \right) \) e divide o retângulo em dois polígonos de mesma área é:
CorretoIncorreto -
Question 11 of 42
11. Question
\(\left( UFJF-MG \right) \) Dados os pontos A = \(\left( 1, 2 \right) \), B = \(\left( 3, 5 \right) \) , C= \(\left( 1, 1 \right) \) e D = \(\left( 2, 3 \right) \), considere as afirmações:
I. Os pontos A, B e D são colineares.
II. Uma reta perpendicular á reta determinada pelos pontos A e B tem coeficiente angular m = \( \frac { -2 }{ 3} \).
III. A distância do ponto A á reta determinada pelos pontos B e C é 10 unidades de comprimento.
É CORRETO afirmar que:
CorretoIncorreto -
Question 12 of 42
12. Question
\(\left( PUC- RJ\right) \) Sejam r e s as retas das equações y = x - 2 e y =\( -\frac {x }{ 2 }\) +\( -\frac {5 }{ 2 } \), respectivamente representados no gráfico abaixo. Seja A o ponto de interseção das retas r e s. Sejam B e C os pontos de interseção de r e s com o eixo horizontal, respectivamente.
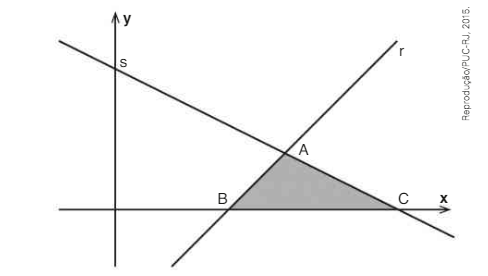
A área do triângulo ABC vale:
CorretoIncorreto -
Question 13 of 42
13. Question
\( \left( UFSM-RS \right) \) A figura mostra um jogo de videogame, em que aviões disparam balas visando atingir o alvo. Quando o avião está no ponto \( \left( 1 , 2 \right) \), dispara uma bala e atinge o alvo na posição \( \left( 3, 0 \right) \).
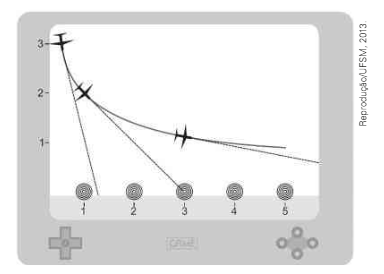
Sendo r a reta determinada pela trajetória da bala, observe as seguintes afirmativas:
I. O ponto P \( \left( \frac {1 }{ 2} ,\frac { 5 }{ 2 } \right) \) pertence a r.
II. A reta r é perpendicular à reta que passa pela origem e pelo ponto médio do segmento \( \left( \bar {AB } \right) \) onde A\( \left( 0,3 \right) \) e B \( \left( 3,0 \right) \).
III. A reta r é paralela á reta s: 2x - 2y + 5 = 0.
Está(ão) correta(s)
CorretoIncorreto -
Question 14 of 42
14. Question
\( \left(UFV-MG \right)\) Sejam a e b números reais tais que a reta de equação \( \left(3b + 4a \right)\) x + 2y + b =0 é paralela ao eixo das abscissas e intersecta bissetriz dos quadrantes pares no ponto de abscissa x = -6. O valor de a é:
CorretoIncorreto -
Question 15 of 42
15. Question
\(\left(UEPB \right) \) Um quadrilátero, cujos vértices são dados por E \(\left(-1, 0\right) \), F \(\left(-2, -2 \right) \), G \(\left(-1, -4 \right) \) e H \(\left(0, -2 \right) \), possui área igual a:
CorretoIncorreto -
Question 16 of 42
16. Question
\( \left( UEPB\right) \) A reta de equação \( \left( x - 2 \right) \)m + \( \left( m-3 \right) \)y + m - 4 = 0, com m constante real, passa pelo ponto P \( \left( 2,0\right) \). Então, seu coeficiente angular é:
CorretoIncorreto -
Question 17 of 42
17. Question
\(\left(Unifesp \right) \) Se P é o ponto de intersecção das retas de equações x- y - 2 = 0 e \( \frac {1 }{ 2} \)x + y = 3, a área do triângulo de vértices A\(\left(0, 3 \right) \), B \(\left(2,0\right) \) e P é:
CorretoIncorreto -
Question 18 of 42
18. Question
\(\left( Enem \right) \) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve á conversão do sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levas esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal ás antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
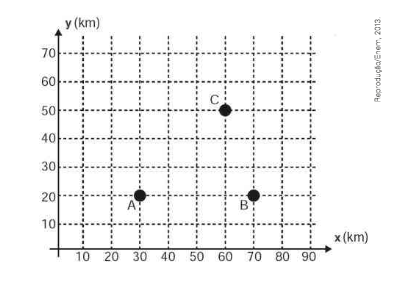
A torre deve estar situada em um local equidistante das três antenas.
O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
CorretoIncorreto -
Question 19 of 42
19. Question
\( \left( Uece\right) \) Em um plano, munido do sistema coordenadas cartesianas usual, as equações 3x - 2y + 6 = 0 e 3x + 4y - 12 = 0, representam duas retas concorrentes. A medida da área da região limitada por essas retas e pelo eixo dos x é:
u.a = unidade de área
CorretoIncorreto -
Question 20 of 42
20. Question
\(\left(PUC-SP \right) \) Suponha que no plano cartesiano mostrado na figura abaixo, em que a unidade de medida nos eixos coordenados é o quilômetro, as retas r e s representam os trajetos percorridos por dois navios \( { N}_{ 1 }\), \( { N}_{ 2 }\), antes de ambos atracarem em uma ilha, localizada no ponto I.
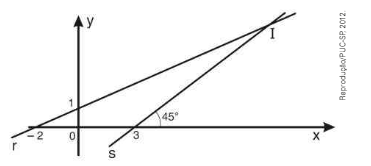
Considerando que, no momento em que \( {N }_{ 1}\) e \( {N }_{ 2}\) se encontravam atracados em I, um terceiro navio, \( {N }_{ 3}\), foi localizado no ponto de coordenadas \(\left(26, 29 \right) \), a quantos quilômetros \( {N }_{ 3}\) distava de I ?
CorretoIncorreto -
Question 21 of 42
21. Question
\( \left( FGV SP \right) \) No plano cartesiano, considere o triângulo de vértices A\( \left( 1,4 \right) \),B\( \left( 4,5 \right) \) e C \( \left( 6,2 \right) \).
A reta suporte da altura relativa ao lado \( \bar { AC} \) intersecta o eixo x no ponto de abscissa:
CorretoIncorreto -
Question 22 of 42
22. Question
\( \left( FGV-SP\right) \) Observe as coordenadas cartesianas de cinco pontos. A \( \left( 0, 100\right) \), B\( \left(0, -100\right) \) , C\( \left( 10, 100\right) \), D\( \left( 10, -100\right) \), E\( \left( 100,0\right) \).
Se a reta de equação reduzida y= mx + n é tal que mn >0 então, dos cinco pontos dados anteriormente, o único que certamente não pertence ao gráfico dessa reta é:
CorretoIncorreto -
Question 23 of 42
23. Question
\( \left( UFRGS RS \right) \) Os pontos A, B, C, D, E e F determinam um hexágono regular ABCDEF de lado 1, tal que o ponto A tem coordenadas \( \left( 1, 0 \right) \) e o ponto D tem coordenadas \( \left( -1, 0 \right) \), como na figura abaixo.
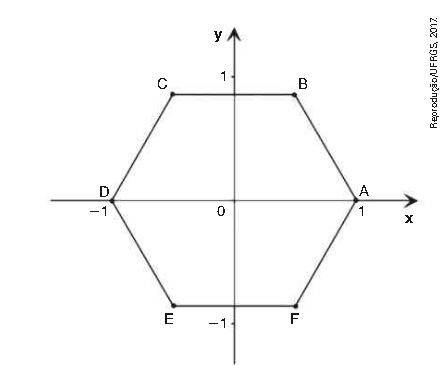
A equação da reta que passa pelos pontos B e D é
CorretoIncorreto -
Question 24 of 42
24. Question
\( \left( Enem \right) \) Uma região de uma fábrica deve ser isolada, pois nela os empregados ficam expostos a riscos de acidentes. Essa região está representada pela porção de cor cinza ( quadrilátero de área S) na figura.
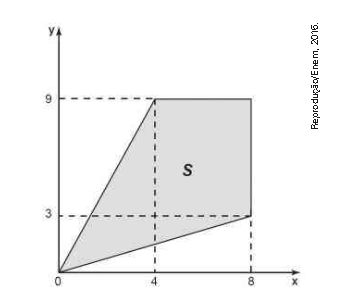
Para que os funcionários sejam orientados sobre a localização da área isolada, cartazes informativos serão afixados por toda a fábrica. Para confeccioná-los, um programador utilizará um software que permite desenhar essa região a partir de um conjunto de desigualdades algébricas. As desigualdades que devem ser utilizadas no referido software, para o desenho da região de isolamento, são
CorretoIncorreto -
Question 25 of 42
25. Question
\( \left(Mac SP \right) \) Na figura, as retas r e s são paralelas.
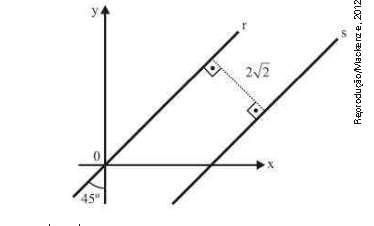
Se \( \left(x,y \right) \) é um ponto s, então x - y vale:
CorretoIncorreto -
Question 26 of 42
26. Question
\( \left(Ufam \right) \) Sejam A \( \left(- 4, 2 \right) \), B \( \left(-8, -8 \right) \), C \( \left(0, 2 \right) \) e D \( \left(4, 12 \right) \) vértices consecutivos de um paralelogramo. A altura relativa ao lado \(\bar {BC } \) deste paralelogramo é igua a:
CorretoIncorreto -
Question 27 of 42
27. Question
\(\left( Insper SP\right) \) No plano cartesiano, a reta r, de coeficiente angular 10, intersecta o eixo y em um ponto de ordenada a. Já a reta s, de coeficiente angular 9, intersecta o eixo y em um ponto de ordenada b. Se as retas r e s intersectam se em um ponto de abscissa 6, então:
CorretoIncorreto -
Question 28 of 42
28. Question
\( \left( FGV SP \right) \) Os pontos A \( \left( 3, -2 \right) \) e C \( \left( 1, 4 \right) \) do plano cartesiano são vértices de um quadrado ABCD cujas diagonais são \( \bar {AC } \) e \( \bar {BD} \). A reta suporte da diagonal \( \bar {BD } \) intersecta o eixo das ordenadas no ponto de ordenada:
CorretoIncorreto -
Question 29 of 42
29. Question
\( \left(UPE \right) \) Qual a medida da área do quadrilátero limitadas pelas retas \( \left(r \right) \) y = 4; \( \left(s \right) \) 3x - y - 2 = 0; \( \left(t \right) \) y = 1 e \( \left(u \right) \) 3x + 2y - 20 = 0?
CorretoIncorreto -
Question 30 of 42
30. Question
\( \left( ITA SP \right) \) Considere os pontos A = \( \left( 0, -1 \right) \), B = \( \left( 0, 5 \right) \) e a reta r: 2x - 3y + 6 - 0. Das afirmações a seguir:
I. d \( \left( A, r \right) \) = d \( \left( B, r \right) \).
II. B é simétrico de A em relação á reta r.
III. \(\bar { AB } \) é a base de um triângulo equilátero ABC, de vértice C\( \left( -3\sqrt { 3,} 2 \right) \) ou C\( \left( 3\sqrt { 3,} 2 \right) \)
CorretoIncorreto -
Question 31 of 42
31. Question
\(\left( PUC SP\right) \) Em um sistema cartesiano ortogonal, em que a unidade de medida nos eixos é o centímetro, considere:
- a reta r, traçada pelo ponto \(\left( 2, 3\right) \) e paralela á bissetriz dos quadrantes ímpares;
- a reta s, traçada pelo ponto \(\left( 2, 5\right) \) e perpendicular a r;
- o segmento \( \bar { OA} \) em que o ponto O é a origem do sistema e A é a intersecção de r e s.
Um ponto M é tomado sobre o segmento \( \bar { OA} \) de modo que OM e MA correspondam ás medidas da hipotenusa e de um dos catetos de um triângulo retângulo \( \triangle \). Se o outro cateto de \( \triangle \) mede 3 cm, a área de superfície, em centímetros quadrados é:
CorretoIncorreto -
Question 32 of 42
32. Question
\( \left(Insper SP \right) \) No plano cartesiano de figura, feito fora de escala, o eixo x representa uma estrada já existente, os pontos A\( \left(8, 2 \right) \) e B\( \left(3,6 \right) \) representam duas cidades e a reta r, de inclinação 45°, representa uma estrada que será construída.
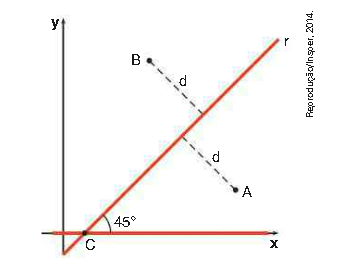
Para que as distâncias da cidade A e da cidade B até a nova estrada sejam iguais, o ponto C, onde a nova estrada intersecta a existente, deverá ter coordenadas:
CorretoIncorreto -
Question 33 of 42
33. Question
\( \left(Mack Sp \right) \)
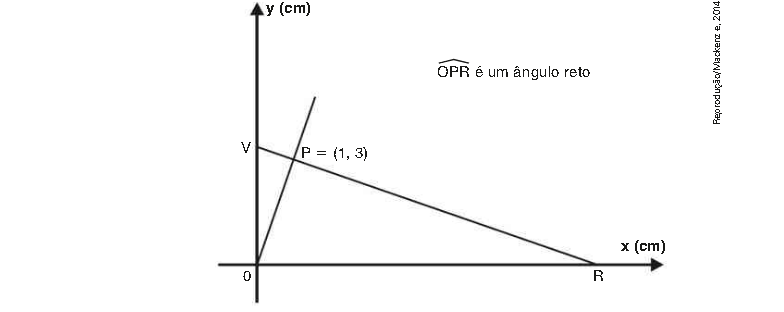
Na figura acima a área, em \( { cm }^{ 2 }\), do triângulo ORV é:
CorretoIncorreto -
Question 34 of 42
34. Question
\( \left( Ufscar SP\right) \) Sabe se, a respeito dos pontos P, Q e R, situados no sistema de coordenadas cartesianas ortogonais, que o ponto P\( \left( x,y\right) \) situa se no 1° quadrante, o ponto Q é simétrico do ponto P em relação ao eixo y e que o ponto R é simétrico do ponto Q em relação á reta y = 1. Pode se concluir, então que as coordenadas do ponto R são:
CorretoIncorreto -
Question 35 of 42
35. Question
\(\left( FGV SP\right) \) O ponto da reta x - 3y = 5 que é mais próximo ao ponto \(\left( 1,3 \right) \) tem coordenadas cuja soma é:
CorretoIncorreto -
Question 36 of 42
36. Question
\(\left( UFRGS RS\right) \) As retas de equações y = ax e y = -x + b interceptam se em um único ponto cujas coordenadas são estritamente negativas.
Então, pode se afirmar que
CorretoIncorreto -
Question 37 of 42
37. Question
\( \left( UFRGS RS \right) \) Os pontos A\( \left(1, 2 \right) \), B\( \left( 6, 2 \right) \) e C são os vértices de um triângulo equilátero, sendo o segmento \( \bar {AB } \) a base deste.
O seno do ângulo formado pelo eixo das abscissas e a reta suporte do lado \( \bar {BC} \) no sentindo anti horário é:
CorretoIncorreto -
Question 38 of 42
38. Question
\( \left(FGV-SP \right) \)No plano cartesiano, a área do polígono determinado pelo sistema de inequações
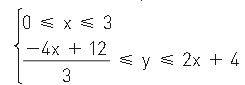 é igual aCorretoIncorreto
é igual aCorretoIncorreto -
Question 39 of 42
39. Question
\( \left( Fatec-SP \right) \) No plano cartesiano representado a seguir, o coeficiente angular da reta \( \overleftarrow { O } \overrightarrow {A } \) é 1, e a área do losango ABCO é 8\( \sqrt { 2 } \). Portanto , o valor de p é:
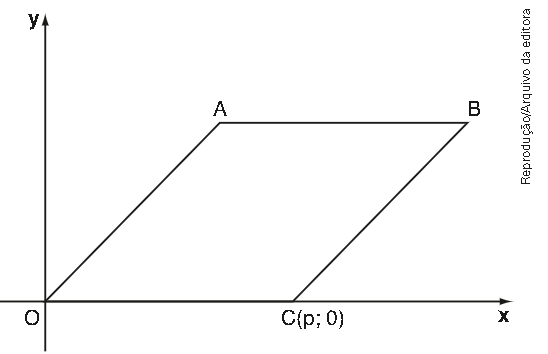 CorretoIncorreto
CorretoIncorreto -
Question 40 of 42
40. Question
\( \left( Uerj \right) \) Considere o gráfico a seguir, em que a área S é limitada pelos eixos coordenados, pela reta r, que passa por A\( \left( 0, 4 \right) \) e B\( \left(2,0 \right) \), e pela reta perpendicular ao eixo x no ponto P\( \left( { x}_{ 0 },0 \right) \), sendo
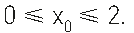
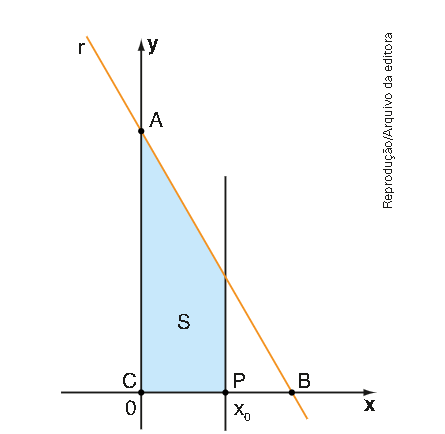
Para que a área S seja a metade da área do triângulo de vértices C\( \left( 0, 0 \right) \),A e B, o valor de \( { x}_{ 0}\) deve ser igua a:
CorretoIncorreto -
Question 41 of 42
41. Question
\( \left( UEMG \right) \) Dadas as equações de reta r: x + y - 6 = 0 e s: 2x - y = 0 em um dado plano cartesiano de centro 0. As retas r e s são concorrentes no ponto P e a reta r intercepta o eixo das abscissas no ponto Q. O volume do sólido formado pela rotação da figura plana formada pelos pontos OPQ em torno do lado \(\bar {OQ } \) é: \( \left ( use \pi = 3 \right)\)
CorretoIncorreto -
Question 42 of 42
42. Question
\( \left( Unifesp \right) \) Num sistema cartesiano ortogonal, são dados os pontos A\( \left( 1,1 \right) \), B\( \left( 5,1 \right) \), C\( \left(6,3 \right) \) e D\( \left( 2, 3 \right) \), vértices de um paralelogramo, e a reta r, de equação r: 3x - 5y - 11 = 0.
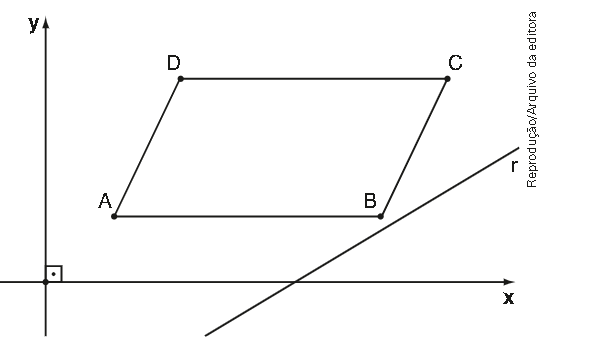
A reta s, paralela á reta r, que divide o paralelogramo ABCD em dois polígonos, de mesma área terá por equação:
CorretoIncorreto
Resolva todas Provas da OBMEP
[vc_tta_tabs color=”orange” active_section=”1″][vc_tta_section title=”2015″ tab_id=”obmep-2015″][vc_column_text]Prova OBMEP 2015 – Nível 1
Prova OBMEP 2015 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2014″ tab_id=”obmep-2014″][vc_column_text]Prova OBMEP 2014 – Nível 1
Prova OBMEP 2014 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2013″ tab_id=”obmep-2013″][vc_column_text]Prova OBMEP 2013 – Nível 1
Prova OBMEP 2013 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2012″ tab_id=”obmep-2012″][vc_column_text]Prova OBMEP 2012 – Nível 1
Prova OBMEP 2012 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2011″ tab_id=”obmep-2011″][vc_column_text]Prova OBMEP 2011 – Nível 1
Prova OBMEP 2011 – Nível 3[/vc_column_text][/vc_tta_section][/vc_tta_tabs]
Pratique outros: Exercicios de Matematica.
Essas foram as questões da prova de matemática do exame da Olimpíada Brasileira de Matemática das Escolas Públicas – OBMEP de 2014, nível 2, ou seja, do 8º e 9º ano do ensino fundamental.
Neste simulado, você resolve a questão e confere a resposta correta com as videoaulas de resolução dos exercícios da equipe do OBMEP. Ao final você recebe sua nota e o desempenho em cada bloco de conteúdo da matemática.
Estude: Tudo sobre Matematica basica.
Aprenda matematica de forma simples e objetiva.
Cadastre-se gratuitamente no Matemática Zup!
E então, conferiu o gabarito? Como se saiu neste simulado de matemática?
Deixe o seu comentário, conversamos logo abaixo.
[wpseo_breadcrumb]
