Provas de Matematica OBMEP 2015 – Nivel 2
[adinserter block=”1″]
Este Simulado de matemática possui todas questões da Prova de Matematica OBMEP 2015 – Nivel 2.
Ao final você receberá sua nota.
Separe uma folha de rascunho e um lápis para fazer os cálculos.
Para ter uma experiência única, CADASTRE-SE GRATUITAMENTE e receba em seu email todos os materiais exclusivos grátis do site.
CLIQUE NO BOTÃO ABAIXO para começar. Boa prova! ?
?
Teste de O ponto Matemática 3ª série
Teste de O ponto Matemática 3ª série online. Ao final receba a sua nota. Conquiste os desafios!
Teste Summary
0 of 24 Perguntas completed
Perguntas:
Information
Você já concluiu o teste antes. Portanto, você não pode reiniciá-lo.
Teste is loading...
You must sign in or sign up to start the teste.
Você precisa primeiro terminar o seguinte:
Resultados
Resultados
0 of 24 Perguntas answered correctly
Seu tempo:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Pontos Médios |
|
| Sua pontuação |
|
Categories
- Not categorized 0%
-
Você precisa melhorar! Você acertou menos que 70% das questões Tente novamente!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Muito bom, Você acertou mais que 70% das questões, você passou!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Parabéns! Você acertou mais que 90% das questões. Siga para os próximos exercícios!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
| Pos. | Nome | Entered on | Pontos | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- Current
- Review
- Answered
- Correto
- Incorreto
-
Question 1 of 24
1. Question
\(\left( Cefet-AM \right)\) Sabe-se que M \(\left( a,b \right)\) é o ponto médio do segmento \(\bar { AB }\) . Se A\(\left( -6, -9 \right)\) e B \(\left( -2, -5\right)\) ,então as coordenadas do ponto M são:
CorretoIncorreto -
Question 2 of 24
2. Question
{ UFPB} Se o ponto P{x -1,3 -2x} do plano está no segundo quadrante do sistema de eixos ortogonais então:
CorretoIncorreto -
Question 3 of 24
3. Question
3.\(\left\{ Cefet-MG \right\} \) Dados os pontos A\( \left\{ 1,1 \right\} \) B \( \left\{ 9,2 \right\} \) e C \( \left\{ 5,8 \right\} \), o triângulo ABC é:
CorretoIncorreto -
Question 4 of 24
4. Question
\(\left\{ Unifesp \right\} \) Um ponto do plano cartesiano é representado pelas coordenadas \(\left\{ x +3y, -x -y \right\} \) e também por \( \left\{ 4 + y, 2x + y \right\} \) em relação a um mesmo sistema de coordenadas. Nestas condições, \( { x }^{ y} \) é igual a:
CorretoIncorreto -
Question 5 of 24
5. Question
\( \left\{PUC-SP \right\} \) Em um sistemas de eixos cartesianos ortogonais, seja o paralelogramo, ABCD em que A \( \left\{5,4 \right\} \), B \( \left\{-3, -2 \right\} \) e C \( \left\{1, -5 \right\} \). Se \( \bar { AC} \) é uma das diagonais desse paralelogramo, a medida da outra diagonal, em unidades de comprimento, é:
CorretoIncorreto -
Question 6 of 24
6. Question
\(\left\{ITA-SP \right\} \) Sejam A\(\left\{ 0, 0 \right\} \), B\(\left\{ 0, 6 \right\} \), C\(\left\{4, 3 \right\} \) vértices de um triângulo. A distância do baricentro deste triângulo ao vértice A, em unidades de distância, é igual a:
CorretoIncorreto -
Question 7 of 24
7. Question
\(\left\{ Ufam \right\}\) A área da figura OABC a seguir representa um terreno com forma de um quadrilátero não convexo, medido em metros quadrados. Podemos afirmar que essa área é:
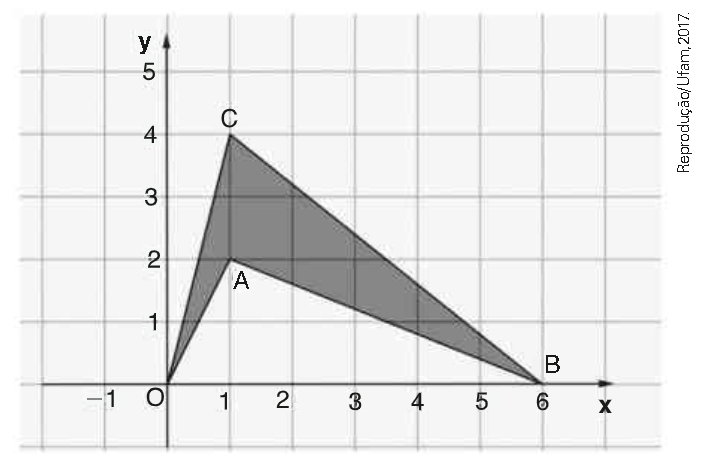 CorretoIncorreto
CorretoIncorreto -
Question 8 of 24
8. Question
\( \left( UEA-AM \right) \) Num plano cartesiano, sabe-se que os pontos A 8\( \left( 1,2 \right) \) e \( \left( 2,3 \right) \) pertecem a uma mesma reta, e que o ponto A está sobre o eixo Oy. O valor da coordenada de A é:
CorretoIncorreto -
Question 9 of 24
9. Question
\( \left( ESPM-SP \right) \) Os pontos 0\( \left(0, 0 \right) \), \( P\left( x, 2 \right) \) e Q \( \left(1, x +1 \right) \) do plano cartesiano são distintos e colineares. A área do quadrado de diagonal \(\bar {PQ } \) vale:
CorretoIncorreto -
Question 10 of 24
10. Question
\(\left(ENEM \right) \) Devido ao aumento do fluxo de passageiros uma empresa de transporte coletivo urbano está fazendo estudos para importação de um novo ponto de parada em uma determinada rota.
A figura mostra o percurso, indicado pelas setas, realizados por um ônibus nessa rota e a localização de dois dos seus atuais pontos de parada representadas por P e Q.
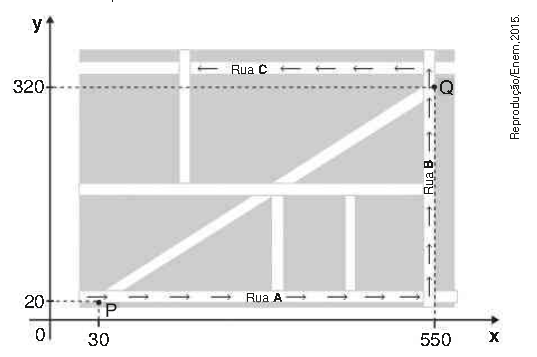
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto de parada são:
CorretoIncorreto -
Question 11 of 24
11. Question
\( \left( Insper-SP \right) \) A figura mostra um tabuleiro de um jogo Batalha Naval, em que André representou três navios nas posições dadas pelas coordenadas B2, B14 e M3. Cada navio está identificado por um quadrado sombreado.
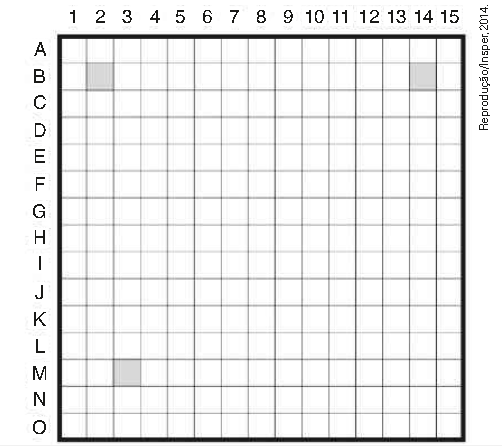
André deseja instalar uma base em um quadrado do tabuleiro cujo centro fique equidistante dos centros dos três quadrados onde foram posicionados os navios. Para isso, a base deverá estar localizada no quadrado de coordenadas:
CorretoIncorreto -
Question 12 of 24
12. Question
\(\left\{Obmep \right\} \) O quadrado da figura tem uma vértice na origem, outro no ponto, \(\left\{10, 7 \right\} \) e um terceiro no ponto \(\left\{a, b \right\} \). Qual é o valor de a + b?
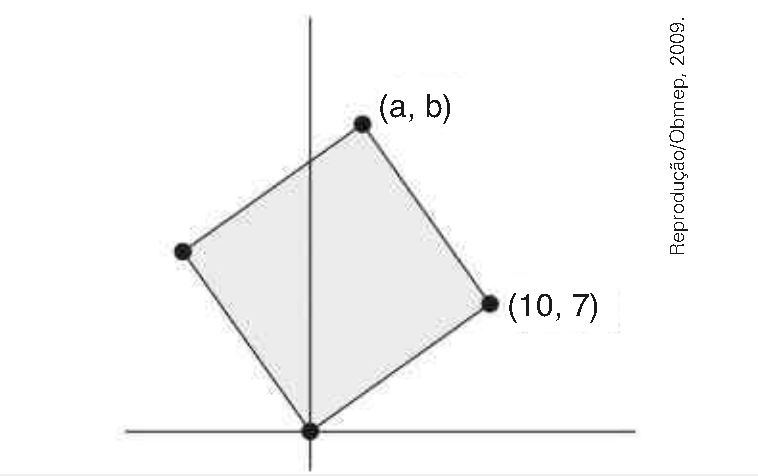 CorretoIncorreto
CorretoIncorreto -
Question 13 of 24
13. Question
\(\left( PUC-RJ \right) \) Se os pontos, A\(\left( 1, 0 \right) \), B\(\left( 1, 0 \right) \), C\(\left( x,y \right) \) são vértices de um triângulo equilátero, então a distância entre A e C é:
CorretoIncorreto -
Question 14 of 24
14. Question
\(\left( PUC-RJ \right) \) Seja de \(\left( P, Q \right) \) a distância entre os pontos P e Q.
Considere A - \(\left( 1, 0 \right) \) e B - \(\left( 1, 0\right) \), pontos do plano.
O número de pontos X - \(\left( x,y \right) \) tais que d\(\left(X,B \right) \) - -\(\frac { 1 }{2 } \)d\(\left( X,A \right) \) - \(\frac { 1 }{2 } \) d\(\left( A,B\right) \) é igual a:
CorretoIncorreto -
Question 15 of 24
15. Question
\(\left(UFRGS-RS \right) \) Em um sistema de coordenadas cartesianas, serão traçados triângulos isósceles.
Os vértices da base do primeiro triângulo são os pontos A \(\left(-1, 2 \right) \) e B \(\left(2, 2 \right) \); os vértices da base do segundo triângulo são C \(\left(3,5 ; 2 \right) \) e D \(\left(6,5; 2 \right) \) o terceiro triângulo tem os vértices de sua base nos pontos E \(\left(8;2 \right) \) e F \(\left(11; 2 \right) \). Prosseguindo com esse padrão de construção , obtém-se uma sequência de triângulos.
Com base nesses dados, é correto afirmar que a abscissa do vértice oposto à base do \({ 18 }^{ º }\) triângulo é:
CorretoIncorreto -
Question 16 of 24
16. Question
\(\left( ENEM\right) \) Uma família resolveu comprar um imóvel num bairro cujas ruas estão representas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal, Desconsidera a largura das ruas.
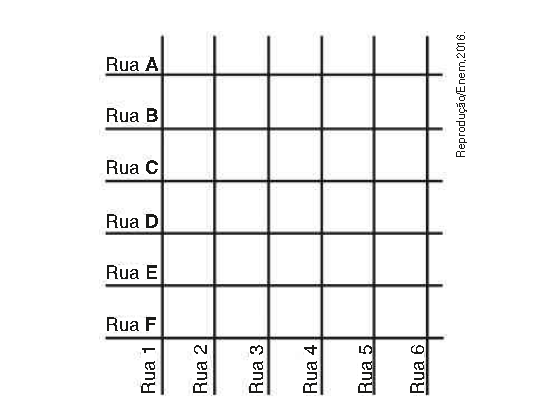
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
CorretoIncorreto -
Question 17 of 24
17. Question
\(\left( UFMG\right) \) Nesta figura, está representado uma quadrado de vértices ABCD:
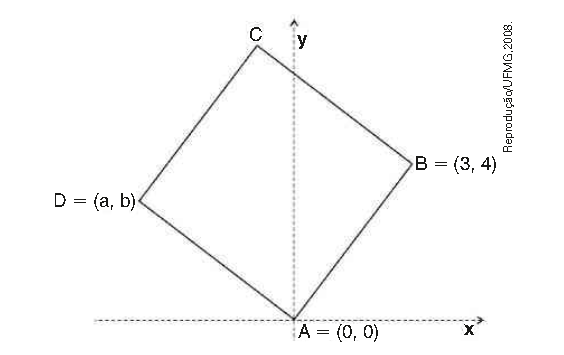
Sabe-se que as coordenadas cartesianas dos pontos A e B são A\(\left(0,0 \right) \) e B\(\left(3,4 \right) \).
Então é CORRETO afirmar que o resultado da soma das coordenadas da vértice D é:
CorretoIncorreto -
Question 18 of 24
18. Question
\(\left( Ufscar-SP\right) \) Um bairro de uma cidade está representando de forma esquemática sobre um plano cartesiano, conforme mostra a área verde na figura.
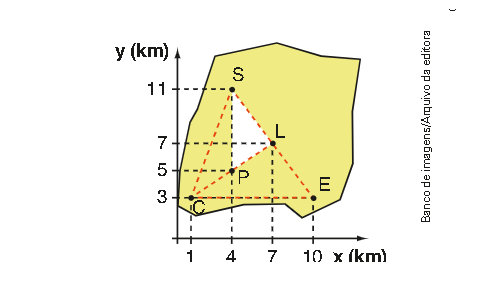
Os pontos C, S e E delimitam a área a ser revitalizada pela prefeitura e, dentro dessa área, o triângulo de vértices P,S e L delimita a área onde será construído um espaço de lazer para a população.
Sabendo-se que todas as coordenadas desse plano cartesiano estão em Km, é correto concluir que a área, em \({ Km }^{2 }\), destinada ao espaço de lazer é:
CorretoIncorreto -
Question 19 of 24
19. Question
\( \left(Fuvest-SP \right) \) Considere o triângulo ABC no plano cartesiano com vértices A = (0,0), B = (3,4) e C =(8, 0) . O retângulo MNPQ tem os vértices M e N sobre o eixo das abscissas, o vértice Q sobre o lado \(\bar { AB } \) e o vértice P sobre o lado \(\bar { BC } \). Dentre todos os retângulos construídos desse modo, o que tem área máxima é aquele em que o ponto P é:
CorretoIncorreto -
Question 20 of 24
20. Question
\(\left( PUC-MG\right) \) Os catetos \(\bar { AC } \) e \(\bar { AB } \) de um triângulo retângulo estão sobre sobre os eixos de um sistema cartesiano. Se M \(\left( -1, 3\right) \) for no ponto médio da hipotenusa \(\bar { BC } \), é correto afirmar que a soma das coordenadas dos vértices desse triângulo é igual a:
CorretoIncorreto -
Question 21 of 24
21. Question
\( \left( PUC-SP \right) \) Dois navios navegavam pelo Oceano Atlântico, supostamente: X, á velocidade constante de 16 milhas por hora , e Y á velocidade constante de 12 milhas por hora. Sabe-se que ás 15 horas de certo dia Y estava exatamente 72 milhas ao sul de X e que, a partir de então, Y navegou em linha reta para o leste, enquanto X navegou em linha reta para o sul, cada qual mantendo suas respectivas velocidades. Nessas condições, ás 17 horas e 15 minutos do mesmo dia, a distância entre X e Y, em milhas era:
CorretoIncorreto -
Question 22 of 24
22. Question
\(\left( Mack-SP \right) \)
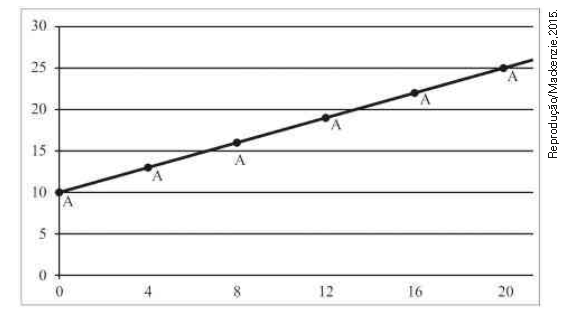
Se, no gráfico acima, os pontos \( { A }_{ n} \) = \(\left(4n, { y }_{ n} \right) \), n = 0,1,2..., estão sobre uma reta e a distância de \( {A}_{ 0 } \) a \( { A }_{ 1} \) a 5, então a soma \({ y }_{ 0}\) + \({ y}_{ 1}\) + \({ y }_{ 2}\) + ... + \({A}_{ 200}\) é igual a :
CorretoIncorreto -
Question 23 of 24
23. Question
\(\left(UFSM-RS \right) \) O uso de fontes de energia limpas e renováveis, como a energia eólica, geométrica e hidráulica, é uma das ações relacionadas com a sustentabilidade que visa diminuir o consumo de combustíveis fósseis, além de preservar os recursos minerais e diminuir a poluição do ar. Em uma estação de energia eólica, os cata-ventos \( { C }_{ 1 } \) , \( { C }_{ 2} \), \( { C }_{ 3 } \), estão dispostos conforme o gráfico a seguir.
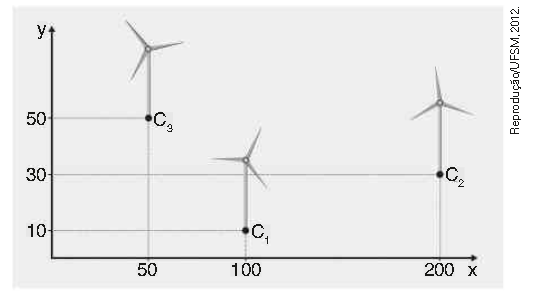
Para que um cata-vento de coordenadas (x,y) esteja alinhado com o cata-vento \( {C }_{ y } \) e com o ponto médio do segmento \( \bar { { C }_{ 2 }{ C }_{ 3} } \), é necessário e suficiente que:
CorretoIncorreto -
Question 24 of 24
24. Question
\(\left( Fatec-SP \right) \) No plano cartesiano da figura, considere que as escalas nos dois eixos coordenados são iguais e que a unidade de medida linear é 1cm . Nele, está representada parte de uma linha poligonal que começa no ponto P\(\left( 0;3 \right) \) e, mantendo-se o mesmo padrão, termina em um ponto Q.
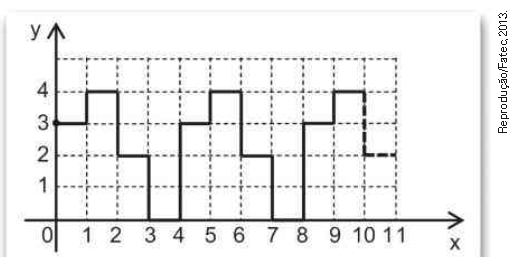
Na figura, a linha poligonal é formada por segmentos de reta
- que são paralelos aos eixos coordenados e
- cujas extremidades têm coordenadas inteiras negativas
Sabendo que o comprimento da linha poligonal, do ponto P até o ponto Q, é igual a 94 cm, as coordenadas do ponto Q são:
CorretoIncorreto
Resolva todas Provas da OBMEP
[vc_tta_tabs color=”orange” active_section=”1″][vc_tta_section title=”2015″ tab_id=”obmep-2015″][vc_column_text]Prova OBMEP 2015 – Nível 1
Prova OBMEP 2015 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2014″ tab_id=”obmep-2014″][vc_column_text]Prova OBMEP 2014 – Nível 1
Prova OBMEP 2014 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2013″ tab_id=”obmep-2013″][vc_column_text]Prova OBMEP 2013 – Nível 1
Prova OBMEP 2013 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2012″ tab_id=”obmep-2012″][vc_column_text]Prova OBMEP 2012 – Nível 1
Prova OBMEP 2012 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2011″ tab_id=”obmep-2011″][vc_column_text]Prova OBMEP 2011 – Nível 1
Prova OBMEP 2011 – Nível 3[/vc_column_text][/vc_tta_section][/vc_tta_tabs]
Pratique outros: Exercicios de Matematica.
Essas foram as questões da prova de matemática do exame da Olimpíada Brasileira de Matemática das Escolas Públicas – OBMEP de 2015, nível 2, ou seja, do 8º e 9º ano do ensino fundamental.
Neste simulado, você resolve a questão e confere a resposta correta com as videoaulas de resolução dos exercícios da equipe do OBMEP. Ao final você recebe sua nota e o desempenho em cada bloco de conteúdo da matemática.
Estude: Tudo sobre Matematica basica.
Aprenda matematica de forma simples e objetiva.
Cadastre-se gratuitamente no Matemática Zup!
E então, conferiu o gabarito? Como se saiu neste simulado de matemática?
Deixe o seu comentário, conversamos logo abaixo.
[wpseo_breadcrumb]

Como faço pra resolver as questões da obmep
ta errado, na primeira, eu respondi 22Kg. E deu como incorreta, e dps apareceu um video exicando outra questão q nem era essa ;-;
é muito bom
é muito bom