Provas de Matematica OBMEP 2015 – Nivel 3
[adinserter block=”1″]
Este Simulado de matemática possui todas questões da Provas de Matematica OBMEP 2015 – Nivel 3.
Ao final você receberá sua nota.
Separe uma folha de rascunho e um lápis para fazer os cálculos.
Para ter uma experiência única, CADASTRE-SE GRATUITAMENTE e receba em seu email todos os materiais exclusivos grátis do site.
CLIQUE NO BOTÃO ABAIXO para começar. Boa prova! ?
?
Teste de Equações e Inequações Matemática 9º ano
Teste de Equações e Inequações Matemática 9º ano online. Ao final receba a sua nota. Conquiste os desafios!
Teste Summary
0 of 25 Perguntas completed
Perguntas:
Information
Você já concluiu o teste antes. Portanto, você não pode reiniciá-lo.
Teste is loading...
You must sign in or sign up to start the teste.
Você precisa primeiro terminar o seguinte:
Resultados
Resultados
0 of 25 Perguntas answered correctly
Seu tempo:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Pontos Médios |
|
| Sua pontuação |
|
Categories
- Not categorized 0%
-
Você precisa melhorar! Você acertou menos que 70% das questões Tente novamente!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Muito bom, Você acertou mais que 70% das questões, você passou!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
-
Parabéns! Você acertou mais que 90% das questões. Siga para os próximos exercícios!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
| Pos. | Nome | Entered on | Pontos | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Current
- Review
- Answered
- Correto
- Incorreto
-
Question 1 of 25
1. Question
(Vunesp) A figura representa um canteiro retangular, cujas medidas de comprimento e de largura, em metros, são, respectivamente, \(x+\sqrt { 16 } \) e \( x-\sqrt { 16 } \).

Para que esse canteiro tenha área de 48 m², o valor de X deverá ser igual a:
CorretoIncorreto -
Question 2 of 25
2. Question
Uma escrivaninha é coberta por um vidro retangular de área 1,28 m². Se o comprimento do vidro é o dobro da largura, então o seu perímetro, em metros, é igual a:
CorretoIncorreto -
Question 3 of 25
3. Question
(Saresp) A equação \(\left( x-3 \right) \cdot \left( x-2 \right) =0 \) é a forma fatorada de:
CorretoIncorreto -
Question 4 of 25
4. Question
Encontre a maior raiz da equação: \( { x }^{ 2 }-\left( 2,333... \right) x+\left( 1,333... \right) =0\)
CorretoIncorreto -
Question 5 of 25
5. Question
A diferença entre a maior e a menor raiz da equação \({ x }^{ 2 }-x-1=\) é:
CorretoIncorreto -
Question 6 of 25
6. Question
Uma das raízes da equação: \({ kx }^{ 2 }-2x+\left( k+2 \right) =0 \) é \(-\frac { 1 }{ 2 } \)
O valor de K é um número:
CorretoIncorreto -
Question 7 of 25
7. Question
(Instituto Embraer-SP) A um terreno quadrado, de lado X, foram anexadas duas regiões retangulares congruentes, conforme mostra a figura, formando um terreno retangular de área igual a 800 m²
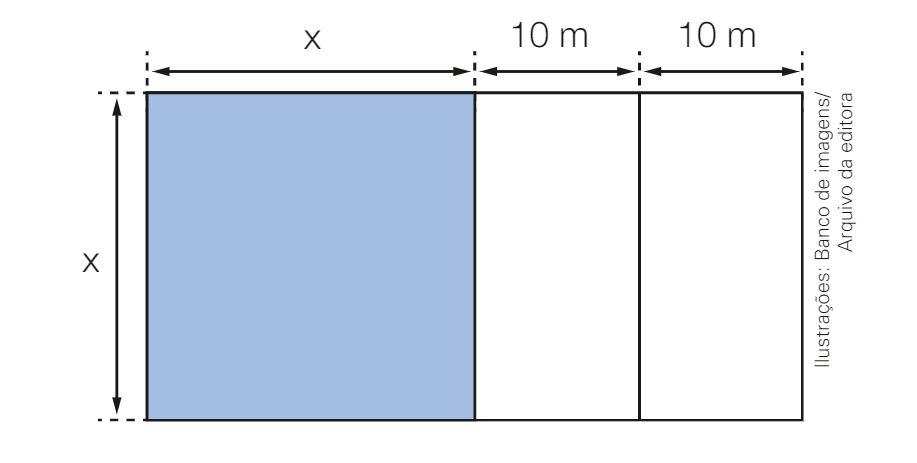
Nessas condições, é correto afirmar que a medida do lado do terreno quadrado original, indicada por X na figura, é, em metros, igual a:
CorretoIncorreto -
Question 8 of 25
8. Question
A equação \(\\ \left( x+5 \right) \left( x+9 \right) =2x+5 \) admite:
CorretoIncorreto -
Question 9 of 25
9. Question
Sabendo que a equação \( { x }^{ 2 }+bx+3=0\) admite raízes reais e que b é um inteiro de 1 a 10, quantas são as possibilidades para b?
CorretoIncorreto -
Question 10 of 25
10. Question
A soma e o produto das raízes da equação \( \left( x+1 \right) \left( x+2 \right) =8x+16\) são, respectivamente:
CorretoIncorreto -
Question 11 of 25
11. Question
A média aritmética e a média geométrica das raízes da equação \( { x }^{ 2 }-10x+16=0\) são raiíes da equação
CorretoIncorreto -
Question 12 of 25
12. Question
Sendo \({ x }_{ 1 } \) e \({ x }_{ 2 } \) as raízes da equação \({ x }^{ 2 }+7x+6=0 \), o valor da expressão \( \left( { x }_{ 1 }+10 \right) \left( { x }_{ 2 }+10 \right) \) é:
CorretoIncorreto -
Question 13 of 25
13. Question
(Fuvest-SP) A equação \({ x }^{ 2 }-x+c=0 \), para um conveniente valor c, admite raízes iguais a:
CorretoIncorreto -
Question 14 of 25
14. Question
Leia o texto abaixo e depois responda.
Era uma vez um soberano num país do Oriente que tinha x esposas e, com cada uma delas, \( \left( x-2 \right) \) filhos. Quando numa batalha a metade das esposas perderam, cada uma, um de seus filhos, ao soberano restaram apenas 44 deles.
Para saber quantas esposas tinha o soberano, qual das equações abaixo devemos resolver?
CorretoIncorreto -
Question 15 of 25
15. Question
A equação \({ x }^{ 2 }+\frac { 1 }{ x+1 } =1+\frac { 1 }{ x+1 } \) admite:
CorretoIncorreto -
Question 16 of 25
16. Question
Se o par (x,y) de números reais e solução de \( \left\{ { x²+y²=5\\ xy=-2} \right\} \) , podemos concluir que \( { \left( x+y \right) }^{ 2 }\) é:
CorretoIncorreto -
Question 17 of 25
17. Question
Na equação \({ x }^{ 4 }+2{ x }^{ 2 }-1=0\), quantas são as raízes reais?
CorretoIncorreto -
Question 18 of 25
18. Question
Um número tem 20 unidades a mais do que sua raiz quadrada. A soma desse número com a sua raiz quadrada dá:
CorretoIncorreto -
Question 19 of 25
19. Question
Um retângulo áureo é aquele em que o comprimento, \(c \), está para a largura, \(l \), assim como a largura, \( l\), está para a diferença entre o comprimento e a largura , \(c-l \):
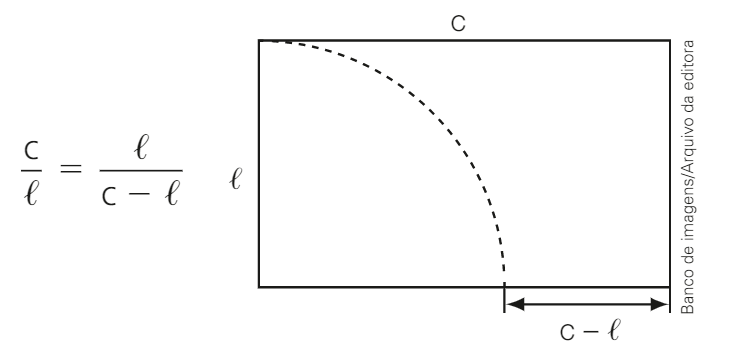
Essa razão, \(\frac { c }{ l } \) foi chamada de razão áurea por Leonardo da Vinci (1445-1514). Qual é o valor exato dessa razão?
CorretoIncorreto -
Question 20 of 25
20. Question
(CTI/Unesp-SP) Um grupo de X professores se reuniu em um restaurante para comemorar o final do ano letivo. A conta, no valor de R$ 720,00, seria inicialmente dividida entre todos, e cada um pagaria Y reais. Depois, decidiu-se que três professores, que aniversariavam naquela semana, não deveriam pagar. Assim, cada um dos demais contribuiu com mais R$ 40,00 e a conta foi paga. A equação que permite calcular corretamente o número de professores desse grupo é:
CorretoIncorreto -
Question 21 of 25
21. Question
A raíz da equação \( x=1+\sqrt { 3x+15 } \) é um número:
CorretoIncorreto -
Question 22 of 25
22. Question
Uma agência de turismo organizou uma excursão para uma turma de estudantes. A despesa total foi de R$ 3.600,00. Como 6 estudantes não puderam ir ao passeio, a parte de cada um aumentou R$ 20,00. Quantos foram ao passeio?
CorretoIncorreto -
Question 23 of 25
23. Question
(Unisa-SP) Uma empresa farmacêutica produz mensalmente 60 000 unidades de carta vacina, que são distribuídas igualmente em X caixas refrigeradas para estocagem. Devido a falhas operacionais ocorridas em certo mês M, cada caixa refrigerada recebeu 500 unidades a menos que o usual, tendo sido necessário usar, nesse mesmo mês, 4 caixas a mais do que usual. Nessas condições, é correto afimar que a quantidade de caixas refrigeradas necessária para acomodar a produção dessa vacina no mês M foi?
CorretoIncorreto -
Question 24 of 25
24. Question
(FGV-SP) Sendo x, y e z números reais tais que \( \\ \frac { y }{ z } =7\quad e\quad \frac { x }{ y } =3\), o valor de \( \frac { x-y }{ y-z } \) é igual a:
CorretoIncorreto -
Question 25 of 25
25. Question
(FGV-RJ) Sejam x e y números reais não nulos tais que \( \frac { 2x+3y }{ x-2y } =-2\). O valor de \(\frac { 3y-2x }{ y-2x } \) é
CorretoIncorreto
Resolva todas Provas da OBMEP
[vc_tta_tabs color=”orange” active_section=”1″][vc_tta_section title=”2015″ tab_id=”obmep-2015″][vc_column_text]Prova OBMEP 2015 – Nível 1
Prova OBMEP 2015 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2014″ tab_id=”obmep-2014″][vc_column_text]Prova OBMEP 2014 – Nível 1
Prova OBMEP 2014 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2013″ tab_id=”obmep-2013″][vc_column_text]Prova OBMEP 2013 – Nível 1
Prova OBMEP 2013 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2012″ tab_id=”obmep-2012″][vc_column_text]Prova OBMEP 2012 – Nível 1
Prova OBMEP 2012 – Nível 3[/vc_column_text][/vc_tta_section][vc_tta_section title=”2011″ tab_id=”obmep-2011″][vc_column_text]Prova OBMEP 2011 – Nível 1
Prova OBMEP 2011 – Nível 3[/vc_column_text][/vc_tta_section][/vc_tta_tabs]
Pratique outros: Exercicios de Matematica.
Essas foram as questões da prova de matemática do exame da Olimpíada Brasileira de Matemática das Escolas Públicas – OBMEP de 2015, nível 3, ou seja, do 1º,2º e 3º ano do ensino médio.
Neste simulado, você resolve a questão e confere a resposta correta com as videoaulas de resolução dos exercícios da equipe do OBMEP. Ao final você recebe sua nota e o desempenho em cada ramo da matemática.
Estude: Tudo sobre Matematica basica.
Aprenda matematica de forma simples e objetiva.
Cadastre-se gratuitamente no Matemática Zup!
E então, conferiu o gabarito? Como se saiu neste simulado de matemática?
Deixe o seu comentário, conversamos logo abaixo.
[wpseo_breadcrumb]

É muito bom acertei todas !!